fix: tracking

README.md

@@ -77,6 +77,6 @@ conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/f
 
 相关文件和介绍在 [logic](https://github.com/ACMClassCourse-2023/PPCA-AIPacMan-2024/tree/main/logic) 文件夹下。
 
-## 前瞻（开发中项目）
-
 ### Tracking
+
+相关文件和介绍在 [tracking](https://github.com/ACMClassCourse-2023/PPCA-AIPacMan-2024/tree/main/tracking) 文件夹下。

tracking/README.md

@@ -36,6 +36,8 @@ python busters.py
 
 #### 贝叶斯网络和因子
 
+[前置芝士](https://github.com/ACMClassCourse-2023/PPCA-AIPacMan-2024/blob/main/docs/bayes.md)
+
 首先，看看 `bayesNet.py` 文件，了解你将要使用的类——贝叶斯网络（BayesNet）和因子（Factor）。你还可以运行这个文件，查看一个贝叶斯网络及其相关因子的示例：`python bayesNet.py`。
 
 你应该查看 `printStarterBayesNet` 函数——其中有一些有用的注释，可以让你的工作更轻松。
@@ -165,3 +167,175 @@ python autograder.py -t test_cases/q4/1-disconnected-eliminate
 首先，填写 `normalize` 方法，该方法将分布中的值规范化，使其总和为1，但保持值的比例不变。使用 `total` 方法找到分布中值的总和。对于空分布或所有值均为零的分布，不做任何操作。请注意，该方法直接修改分布，而不是返回一个新分布。
 
 其次，填写 `sample` 方法，该方法从分布中抽取一个样本，其中抽取某个键的概率与其对应值成比例。假设分布非空，并且所有值不全为零。请注意，在调用此方法之前，分布不必一定是规范化的。你可能会发现Python内置的 `random.random()` 函数对于这个问题很有用。
+
+#### Q5b: Observation Probability
+
+在这个问题中，你将在 `inference.py` 中的 `InferenceModule` 基类中实现 `getObservationProb` 方法。该方法接受一个观测值（即到鬼魂距离的噪声读数）、吃豆人的位置、鬼魂的位置和鬼魂监狱的位置，并返回给定吃豆人位置和鬼魂位置的噪声距离读数的概率。换句话说，我们希望返回
+$P(\text{noisyDistance} \mid \text{pacmanPosition}, \text{ghostPosition})$
+
+距离传感器在给定吃豆人到鬼魂的真实距离情况下对距离读数具有概率分布。该分布由函数 `busters.getObservationProbability(noisyDistance, trueDistance)` 建模，该函数返回
+$P(\text{noisyDistance} \mid \text{trueDistance})$
+该函数已经为你提供。你应该使用此函数来帮助你解决问题，并使用提供的 `manhattanDistance` 函数来查找吃豆人位置和鬼魂位置之间的距离。
+
+但是，我们还需要处理监狱的特殊情况。具体来说，当我们捕获一个鬼魂并将其送到监狱位置时，我们的距离传感器确定性地返回 None，而不是其他任何值（当且仅当鬼魂在监狱中时，观测值为 None）。其一个结果是，如果鬼魂的位置是监狱位置，那么观测值为 None 的概率是1，其他任何值的概率是0。确保在你的实现中处理这种特殊情况；每当鬼魂在监狱中，以及每当观测值为 None 时，我们实际上有一套不同的规则。
+
+要测试你的代码并运行这个问题的自动评分器，请执行：
+
+```
+python autograder.py -q q5
+```
+
+#### Q6: Exact Inference Observation
+
+在这个问题中，你将在 `inference.py` 中的 `ExactInference` 类中实现 `observeUpdate` 方法，以根据吃豆人传感器的观测值正确更新代理对鬼魂位置的信念分布。你正在实现观察新证据的在线信念更新。对于这个问题，在接收到传感器读数后，`observeUpdate` 方法应更新地图上每个位置的信念。你应该遍历 `self.allPositions` 变量，其中包括所有合法位置加上特殊的监狱位置。信念表示鬼魂在特定位置的概率，并作为一个 `DiscreteDistribution` 对象存储在名为 `self.beliefs` 的字段中，你需要更新它。
+
+在编写代码之前，写下你要解决的推理问题的方程。你应该使用你在上一个问题中编写的 `self.getObservationProb` 函数，该函数返回给定吃豆人位置、潜在鬼魂位置和监狱位置的观测概率。你可以使用 `gameState.getPacmanPosition()` 获取吃豆人的位置，使用 `self.getJailPosition()` 获取监狱位置。
+
+在吃豆人显示中，高后验信念用亮颜色表示，而低信念用暗颜色表示。你应该从一个大的信念云开始，随着更多证据的积累，逐渐缩小。在观看测试用例时，确保你理解方格是如何收敛到最终颜色的。
+
+注意：你的 `busters` 代理对他们跟踪的每个鬼魂都有一个单独的推理模块。这就是为什么即使板上有多个鬼魂，如果你在 `observeUpdate` 函数中打印一个观测值，你也只能看到一个数字。
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q6
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q6 --no-graphics
+```
+
+#### Q7: Exact Inference with Time Elapse
+
+在前一个问题中，你实现了基于吃豆人的观测进行信念更新。幸运的是，吃豆人的观测并不是他关于鬼魂可能位置的唯一信息来源。吃豆人还知道鬼魂的移动方式，即鬼魂不能穿过墙壁或在一个时间步内移动超过一个格子。
+
+为了理解这对吃豆人有何帮助，考虑以下场景：有一个吃豆人和一个鬼魂。吃豆人收到很多观测，表明鬼魂非常接近，但随后有一个观测表明鬼魂非常远。这个表明鬼魂非常远的读数很可能是一个错误的传感器导致的。吃豆人关于鬼魂移动方式的先验知识将减少这个读数的影响，因为吃豆人知道鬼魂不可能在一次移动中移动那么远。
+
+在这个问题中，你将在 `ExactInference` 类中实现 `elapseTime` 方法。对于这个问题，时间步的流逝应该更新地图上每个位置的信念。你的代理可以通过 `self.getPositionDistribution` 获取鬼魂的行动分布。为了获取给定其先前位置的鬼魂的新位置分布，使用以下代码行：
+
+```
+newPosDist = self.getPositionDistribution(gameState, oldPos)
+```
+
+其中 `oldPos` 指的是鬼魂之前的位置。`newPosDist` 是一个 `DiscreteDistribution` 对象，对于 `self.allPositions` 中的每个位置 `p`，`newPosDist[p]` 表示在时间 `t + 1` 时，鬼魂在位置 `p` 的概率，前提是鬼魂在时间 `t` 时位于位置 `oldPos`。请注意，这个调用可能相当耗时，所以如果你的代码超时，可以考虑是否可以减少对 `self.getPositionDistribution` 的调用次数。
+
+在编写任何代码之前，写下你要解决的推理问题的方程。为了单独测试你的预测实现与前一个问题中的更新实现，这个问题不会使用你的更新实现。
+
+由于吃豆人没有观测到鬼魂的行动，这些行动不会影响吃豆人的信念。随着时间的推移，吃豆人的信念将反映他认为鬼魂最可能出现的位置，这些位置是根据棋盘的几何结构和鬼魂的合法移动推测的，而吃豆人已经知道这些信息。
+
+在这个问题的测试中，我们有时会使用一个随机移动的鬼魂，有时会使用 `GoSouthGhost`。这个鬼魂倾向于向南移动，因此随着时间的推移，在没有任何观测的情况下，吃豆人的信念分布应该开始集中在棋盘的底部。要查看每个测试用例使用的鬼魂，可以查看 `.test` 文件。
+
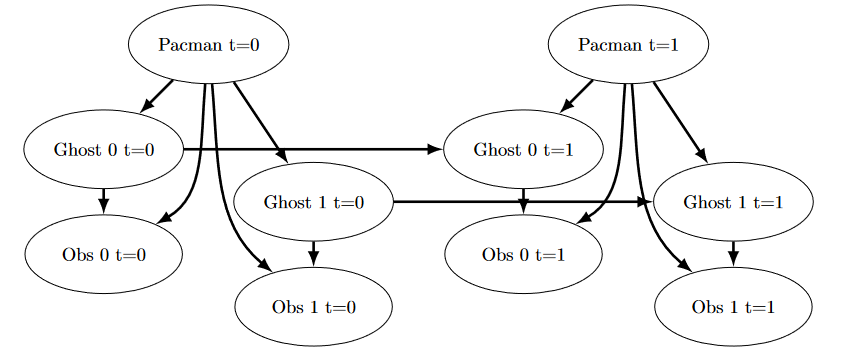
+下图显示了贝叶斯网络/隐马尔可夫模型中发生的情况。然而，你应该依赖上面的描述来进行实现，因为某些部分已经为你实现（即 `getPositionDistribution` 被抽象为
+$ P(G_{t+1} \mid gameState, G_t) $）。
+
+![](https://inst.eecs.berkeley.edu/~cs188/sp24/assets/projects/busters_hmm_time_elapse.png)
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q7
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q7 --no-graphics
+```
+
+在观看自动评分器输出时，请记住，较亮的方格表示吃豆人认为鬼魂更有可能占据该位置，而较暗的方格表示鬼魂不太可能占据该位置。对于哪些测试用例，你注意到方格的阴影出现差异？你能解释为什么一些方格变亮而一些方格变暗吗？
+
+#### Q8: Exact Inference Full Test
+
+现在，吃豆人知道如何在确定鬼魂位置时利用他的先验知识和观测，他准备自己去追捕鬼魂。我们将结合使用你的 `observeUpdate` 和 `elapseTime` 实现来保持更新的信念分布，并且你的简单贪婪代理将在每个时间步基于最新的分布选择一个行动。在简单的贪婪策略中，吃豆人假设每个鬼魂都在他认为的最可能的位置，然后朝最近的鬼魂移动。到目前为止，吃豆人是通过随机选择一个有效动作来移动的。
+
+在 `bustersAgents.py` 中实现 `GreedyBustersAgent` 的 `chooseAction` 方法。你的代理应首先找到每个尚未被捕获的鬼魂的最可能位置，然后选择一个最小化到最近鬼魂的迷宫距离的动作。
+
+要查找任意两个位置 `pos1` 和 `pos2` 之间的迷宫距离，请使用 `self.distancer.getDistance(pos1, pos2)`。要查找一个位置在执行一个动作后的后继位置：
+
+```
+successorPosition = Actions.getSuccessor(position, action)
+```
+
+你提供了 `livingGhostPositionDistributions`，这是一个 `DiscreteDistribution` 对象的列表，代表每个尚未被捕获的鬼魂的位置信念分布。
+
+如果实现正确，你的代理应该在 `q8/3-gameScoreTest` 中以至少8次超过700分的成绩赢得10次游戏中的游戏。注意：自动评分器也将直接检查你的推理的正确性，但游戏结果是一个合理的健全性检查。
+
+我们可以通过对前面的图进行如下修改来表示我们的贪婪代理的工作原理：
+
+![](https://inst.eecs.berkeley.edu/~cs188/sp24/assets/projects/busters_greedy_pacman.png)
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q8
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q8 --no-graphics
+```
+
+#### Q9: Approximate Inference Initialization and Beliefs
+
+近来，近似推理在鬼魂猎人中非常流行。在接下来的几个问题中，你将实现一个用于追踪单个鬼魂的粒子滤波算法。
+
+首先，在 `inference.py` 中的 `ParticleFilter` 类中实现 `initializeUniformly` 和 `getBeliefDistribution` 函数。在这个推理问题中，一个粒子（样本）是一个鬼魂的位置。注意，对于初始化，粒子应该均匀（而不是随机）分布在合法位置上，以确保均匀的先验分布。我们建议考虑如何使用模运算符来实现 `initializeUniformly`。
+
+请注意，你存储粒子的变量必须是一个列表。列表只是一组无权重的变量（在这种情况下是位置）。将粒子存储为任何其他数据类型（如字典）是不正确的，会产生错误。然后，`getBeliefDistribution` 方法将粒子列表转换为一个 `DiscreteDistribution` 对象。
+
+要测试你的代码并运行这个问题的自动评分器，请执行：
+
+```
+python autograder.py -q q9
+```
+
+#### Q10: Approximate Inference Observation
+
+接下来，我们将在 `inference.py` 中的 `ParticleFilter` 类中实现 `observeUpdate` 方法。该方法在 `self.particles` 上构建一个权重分布，其中一个粒子的权重是给定吃豆人位置和该粒子位置的观测概率。然后，我们从这个加权分布中重新采样以构建我们的新粒子列表。
+
+你应该再次使用 `self.getObservationProb` 函数来找到给定吃豆人位置、潜在鬼魂位置和监狱位置的观测概率。`DiscreteDistribution` 类的 `sample` 方法也将很有用。提醒一下，你可以使用 `gameState.getPacmanPosition()` 获取吃豆人的位置，使用 `self.getJailPosition()` 获取监狱位置。
+
+正确的实现必须处理一个特殊情况。当所有粒子都获得零权重时，应通过调用 `initializeUniformly` 重新初始化粒子列表。`DiscreteDistribution` 的 `total` 方法可能会有用。
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q10
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q10 --no-graphics
+```
+
+#### Q11: Approximate Inference with Time Elapse
+
+在 `inference.py` 中的 `ParticleFilter` 类中实现 `elapseTime` 函数。该函数应构建一个新的粒子列表，该列表对应于 `self.particles` 中的每个现有粒子前进一个时间步，然后将这个新列表分配回 `self.particles`。完成后，你应该能够像精确推理一样有效地追踪鬼魂。
+
+请注意，在这个问题中，我们将分别测试 `elapseTime` 函数，以及结合 `elapseTime` 和 `observe` 的粒子滤波器的完整实现。
+
+如同 `ExactInference` 类中的 `elapseTime` 方法一样，你应该使用：
+
+```python
+newPosDist = self.getPositionDistribution(gameState, oldPos)
+```
+
+这行代码获取给定鬼魂先前位置（`oldPos`）的新位置分布。`DiscreteDistribution` 类的 `sample` 方法也将很有用。
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```python
+python autograder.py -q q11
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```python
+python autograder.py -q q11 --no-graphics
+```
+
+请注意，即使没有图形，这个测试也可能需要几分钟才能运行完毕。