Merge remote-tracking branch 'upstream/main'

README.md

@@ -77,6 +77,6 @@ conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/f
 
 相关文件和介绍在 [logic](https://github.com/ACMClassCourse-2023/PPCA-AIPacMan-2024/tree/main/logic) 文件夹下。
 
-## 前瞻（开发中项目）
+### Tracking
 
-### Tracking
+相关文件和介绍在 [tracking](https://github.com/ACMClassCourse-2023/PPCA-AIPacMan-2024/tree/main/tracking) 文件夹下。

docs/bayes.md

@@ -0,0 +1,53 @@
+# 贝叶斯网络
+
+## 介绍
+
+贝叶斯网络是一种概率图式模型，通过对随机变量构建有向无环图捕捉其概率分布。更具体地，你的任务为通过条件概率表来完成指定的查询，即给定先验概率 $P(Q)$ 和条件概率 $P(E|Q)$, 求解后验概率 $P(Q|e)$. 为了解决这一问题，我们可以构建联合分布
+
+$$ P(EQ) = P(E|Q) P(Q) $$
+
+再计算
+
+$$ P(Q|e) = \frac{P(Qe)}{P(e)} = \frac{P(Qe)}{\sum_{q} P(qe)} $$
+
+这样就可以通过联合概率分布来计算后验概率。这一实现存在两个很大的问题：
+1. 完整的联合分布概率表的大小与事件个数呈指数关系（为什么？），导致存储与计算开销太大。
+2. 先验地估计所有信息是困难的。
+
+为此我们考察使用条件概率分布进行推理，即使用贝叶斯公式：
+
+$$ P(Q|e) = \frac{P(e|Q) P(Q)}{\sum_{q} P(e|q) P(q)} $$
+
+这是贝叶斯网络背后的动机：一种使用简单的局部分布（条件概率）描述复杂联合分布（模型）的技术。我们描述变量如何在局部相互作用，并将这些作用组合建模全局的间接相互作用。
+
+## 栗子
+
+在使用 Google 搜索时，当你不小心输入一个不存在的单词时，搜索引擎会提示你是不是要输入某一个正确的单词。Google的拼写检查基于贝叶斯方法。下面我们就来看看，怎么利用贝叶斯方法，实现"拼写检查"的功能。
+
+用户输入一个单词时，可能拼写正确，也可能拼写错误。如果把拼写正确的情况记做c（代表correct），拼写错误的情况记做 w（代表wrong），那么“拼写检查”要做的事情就是：在发生 w 的情况下，试图推断出 c。换言之，已知w，然后在若干个备选方案中，找出可能性最大的那个 $c$, 也就是求 $P(c|w)=P(w|c)P(c)/P(w)$ 的最大值，故只需考察 $\operatorname{argmax}_{c} P(w|c)P(c)$ 即可。
+
+![](images/bayes.png)
+
+上面是一个实际的贝叶斯网络的例子，其中每个节点代表一个事件，节点对应的表即为贝叶斯网络中存储的信息，若我们想要计算 $ P(+w \mid +s, -g) $，则有：
+
+$$ P(+w \mid +s, -g) = \frac{P(+w, +s, -g)}{P(+s, -g)} $$
+
+（链式规则）
+
+$$ P(+w, +s, -g) = \sum_h P(h, +w, +s, -g) $$
+
+（边缘化）
+
+$$ \sum_{h, w} P(h, w, +s, -g) = \sum_h P(h)P(+w \mid h)P(+s \mid +w)P(-g \mid +w) $$
+
+（联合概率分布 = 边缘概率分布的乘积）
+$$
+\begin{aligned}
+P(+w \mid +s, -g) &= \frac{P(+w, +s, -g)}{P(+s, -g)} \quad (\text{条件概率}) \\
+&= \frac{\sum_h P(h, +w, +s, -g)}{\sum_{h, w} P(h, w, +s, -g)} \quad (\text{联合分布转边缘分布}) \\
+&= \frac{\sum_h P(h)P(+w \mid h)P(+s \mid +w)P(-g \mid +w)}{\sum_{h,w} P(h)P(w
+\mid h)P(+s \mid w)P(-g \mid w)} \quad (\text{转为条件概率的乘积}) \\
+&= \frac{0.1 \times 0.667 \times 0.4 \times 0.75 + 0.9 \times 0.25 \times 0.4 \times 0.75}{0.1 \times 0.667 \times 0.4 \times 0.75 + 0.9 \times 0.25 \times 0.4 \times 0.75 + 0.1 \times 0.333 \times 0.2 \times 0.5 + 0.9 \times 0.75 \times 0.2 \times 0.5} \\
+&= 0.553
+\end{aligned}
+$$

tracking/README.md

@@ -0,0 +1,341 @@
+#### 介绍
+
+> 我能听到你的声音，幽灵。
+逃跑并不能让你逃脱我的
+粒子滤波器！
+
+帕克曼一生都在逃离鬼魂，但事情并不总是这样。传说许多年前，帕克曼的曾祖父帕克曼爷爷学会了猎杀鬼魂。然而，他被自己的力量蒙蔽了双眼，只能通过鬼魂的撞击声和叮当声来追踪它们。
+
+在这个项目中，你将设计 Pacman agent，使用传感器来定位和吃掉隐形幽灵。您将从定位单个静止的幽灵进步到以无情的效率猎杀多个移动幽灵群。
+
+你需要补全的代码文件有：
+- `bustersAgents.py`
+- `inference.py`: 用于利用鬼魂的声音来追踪鬼魂随时间变化的代码。
+- `factorOperations.py`: 计算新的联合或边值化概率表的操作。
+
+你可以阅读并参考来帮助你实现代码的文件有：
+- `bayesNet.py`: `BayesNet` 和 `Factor` 类。
+
+你可以忽略其他支持文件。
+
+#### Ghostbusters(捉鬼敢死队) and Bayes Nets
+
+在《捉鬼敢死队》中，目标是追捕那些处于惊恐状态（能吃）但看不见的鬼魂。 Pacman 一如既往地足智多谋，他装备了声纳（耳朵），可以提供到每个鬼魂的曼哈顿距离的噪声读数。当吃豆人吃掉所有鬼魂时，游戏结束。要开始游戏，可以使用键盘进行操作。
+
+```
+python busters.py
+```
+
+彩色方块表示根据提供给吃豆人的噪声距离读数，每个鬼魂可能出现的位置。显示底部的噪声距离总是非负的，并且总是与真实距离相差 7 以内。距离读数的概率随着与真实距离的差异呈指数下降。
+
+在这个项目中，你的主要任务是实现推理以追踪鬼魂。对于上面的基于键盘的游戏，默认为你实现了一种粗略的推理形式：所有鬼魂可能存在的方格都被鬼魂的颜色遮蔽。显然，我们希望能更好地估计鬼魂的位置。幸运的是，贝叶斯网络为我们提供了强大的工具，能够最大限度地利用我们拥有的信息。在这个项目的其余部分中，你将使用贝叶斯网络实现精确和近似推理算法。这个项目具有挑战性，因此我们鼓励你尽早开始并在必要时寻求帮助。
+
+在使用自动评分器观看和调试代码时，了解自动评分器的工作原理将很有帮助。这个项目中有两种类型的测试，可以通过 `test_cases` 文件夹子目录中的 `.test` 文件来区分。对于 `DoubleInferenceAgentTest` 类的测试，你将看到代码生成的推理分布的可视化，但所有吃豆人的动作都将根据工作人员实现的动作预先选择。这是为了允许将你的分布与工作人员的分布进行比较。第二种测试是 `GameScoreTest`，在这种测试中，你的 `BustersAgent` 将实际为吃豆人选择动作，你将观看你的吃豆人游戏并获胜。
+
+在这个项目中，如果运行带图形的测试，自动评分器有时可能会超时。为了准确判断你的代码是否足够高效，你应该使用 `--no-graphics` 标志运行测试。如果使用此标志自动评分器通过了测试，即使带图形的自动评分器超时，你也会获得满分。
+
+#### 贝叶斯网络和因子
+
+[前置芝士](https://github.com/ACMClassCourse-2023/PPCA-AIPacMan-2024/blob/main/docs/bayes.md)
+
+首先，看看 `bayesNet.py` 文件，了解你将要使用的类——贝叶斯网络（BayesNet）和因子（Factor）。你还可以运行这个文件，查看一个贝叶斯网络及其相关因子的示例：`python bayesNet.py`。
+
+你应该查看 `printStarterBayesNet` 函数——其中有一些有用的注释，可以让你的工作更轻松。
+
+该函数创建的贝叶斯网络如下所示：
+
+(Raining –> Traffic <– Ballgame)
+
+下面是术语的摘要：
+
+**贝叶斯网络（Bayes Net）**：这是一个将概率模型表示为有向无环图（DAG）和一组条件概率表（每个变量一个）的表示。上面的交通贝叶斯网络是一个示例。
+
+**因子（Factor）**：这存储了一个概率表，尽管表中条目的总和不一定是1。因子的通用形式是
+$ f(X_1, \ldots, X_m, y_1, \ldots, y_n \mid Z_1, \ldots, Z_p, w_1, \ldots, w_q) $
+请记住，小写变量已经被赋值。对于每个可能的 $X_i$ 和 $Z_j$ 变量的赋值，因子存储一个数字。$Z_j$ 和 $w_k$ 变量被称为条件变量，而 $X_i$ 和 $y_l$ 变量是非条件变量。
+
+**条件概率表（CPT）**：这是一个满足两个属性的因子：
+1. 条目的总和对于每个条件变量的赋值必须为1。
+2. 只有一个非条件变量。交通贝叶斯网络存储了以下CPT：
+$ P(Raining), P(Ballgame), P(Traffic \mid Ballgame, Raining) $
+
+####  Q1: Bayes Net Structure
+
+请在 `inference.py` 中实现 `constructBayesNet` 函数。它构建了一个具有以下结构的空贝叶斯网络。一个贝叶斯网络在没有实际概率的情况下是不完整的，但因子由工作人员代码单独定义和分配；你不需要担心这些。如果你感兴趣，可以在 `bayesNet.py` 中查看 `printStarterBayesNet` 的工作示例。阅读这个函数对于完成这个问题也很有帮助。
+
+简化的捉鬼世界是根据以下贝叶斯网络生成的：
+
+![Bayes Net](https://inst.eecs.berkeley.edu/~cs188/sp24/assets/projects/busters_bayes_net_simplified.png)
+
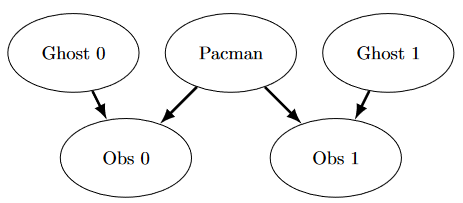
+这个看起来很复杂，但不用担心！我们会一步一步来。正如 `constructBayesNet` 代码中所描述的那样，我们通过列出所有变量、它们的值以及它们之间的边来构建空结构。这个图显示了变量和边，但它们的域是什么呢？
+- 根据图添加变量和边。
+- 吃豆人和两个鬼魂可以在网格中的任何地方（我们在这里忽略墙壁）。为这些添加所有可能的位置元组。
+- 这里的观察值是非负的，等于吃豆人与鬼魂之间的曼哈顿距离 
+$\pm$ 噪声。
+
+评分：要测试和调试你的代码，请运行
+
+```
+python autograder.py -q q1
+```
+
+#### Q2: Join Factors
+
+请在 `factorOperations.py` 中实现 `joinFactors` 函数。该函数接收一个因子列表并返回一个新因子，其概率条目是输入因子对应行的乘积。
+
+`joinFactors` 可以用作乘积规则，例如，如果我们有一个形式为 $P(X \mid Y)$ 的因子和另一个形式为 $P(Y)$ 的因子，那么合并这些因子将得到 \(P(X, Y)\)。因此，`joinFactors` 允许我们为条件变量（在本例中是 \(Y\)）加入概率。但是，你不应该假设 `joinFactors` 只对概率表调用——也可以对行和不等于1的因子调用 `joinFactors`。
+
+要测试和调试你的代码，请运行
+
+```
+python autograder.py -q q2
+```
+
+在调试期间运行特定测试可能会很有用，可以只看到一组因子的输出。例如，要仅运行第一个测试，请运行：
+
+```
+python autograder.py -t test_cases/q2/1-product-rule
+```
+
+提示和观察：
+
+1. 你的 `joinFactors` 应返回一个新因子。
+2. 以下是 `joinFactors` 可以执行的操作示例：
+   - $ \text{joinFactors}(P(X \mid Y), P(Y)) = P(X, Y) $
+   - $ \text{joinFactors}(P(V, W \mid X, Y, Z), P(X, Y \mid Z)) = P(V, W, X, Y \mid Z) $
+   - $ \text{joinFactors}(P(X \mid Y, Z), P(Y)) = P(X, Y \mid Z) $
+   - $ \text{joinFactors}(P(V \mid W), P(X \mid Y), P(Z)) = P(V, X, Z \mid W, Y) $
+
+3. 对于一般的 `joinFactors` 操作，返回的因子中哪些变量是非条件变量？哪些变量是条件变量？
+4. 因子(`Factor`)存储一个 `variableDomainsDict`，它将每个变量映射到它可以取的值（其域）列表。因子从其实例化的贝叶斯网络(`BayesNet`)获取其 `variableDomainsDict`。因此，它包含贝叶斯网络的所有变量，而不仅仅是因子中使用的非条件和条件变量。对于这个问题，你可以假设所有输入因子都来自同一个贝叶斯网络，因此它们的 `variableDomainsDict` 都是相同的。
+
+#### Q3: Eliminate (not ghosts yet)
+
+请在 `factorOperations.py` 中实现 `eliminate` 函数。它接收一个因子和一个要消除的变量，并返回一个不包含该变量的新因子。这对应于对因子中仅在被消除变量的值上有所不同的所有条目求和。
+
+要测试和调试你的代码，请运行
+
+```
+python autograder.py -q q3
+```
+
+在调试期间运行特定测试可能会很有用，可以只看到一组因子的输出。例如，要仅运行第一个测试，请运行：
+
+```
+python autograder.py -t test_cases/q3/1-simple-eliminate
+```
+
+提示和观察：
+
+1. 你的 `eliminate` 应返回一个新因子(`Factor`)。
+2. `eliminate` 可以用于从概率表中边缘化变量。例如：
+   - $ \text{eliminate}(P(X, Y \mid Z), Y) = P(X \mid Z) $
+   - $ \text{eliminate}(P(X, Y \mid Z), X) = P(Y \mid Z) $
+
+3. 对于一般的 `eliminate` 操作，返回的因子中哪些变量是非条件变量？哪些变量是条件变量？
+4. 请记住，因子(`Factor`)存储原始贝叶斯网络(`BayesNet`)的 `variableDomainsDict`，而不仅仅是它们使用的非条件和条件变量。因此，返回的因子应具有与输入因子相同的 `variableDomainsDict`。
+
+#### Q4: Variable Elimination
+
+请在 `inference.py` 中实现 `inferenceByVariableElimination` 函数。它回答一个概率查询，该查询使用贝叶斯网络(`BayesNet`)表示，包含一个查询变量列表和证据。
+
+评分：要测试和调试你的代码，请运行
+
+```
+python autograder.py -q q4
+```
+
+在调试期间运行特定测试可能会很有用，可以只看到一组因子的输出。例如，要仅运行第一个测试，请运行：
+
+```
+python autograder.py -t test_cases/q4/1-disconnected-eliminate
+```
+
+提示和观察：
+
+1. **算法应该迭代消除顺序中的隐藏变量**，对这些变量执行合并和消除操作，直到只剩下查询变量和证据变量。
+2. **输出因子的概率之和应为1**，这样它才是一个条件在证据上的真正条件概率。
+3. 查看 `inferenceByEnumeration` 函数在 `inference.py` 中的示例，了解如何使用所需的函数。（提醒：枚举推理首先对所有变量进行合并，然后消除所有隐藏变量。相比之下，变量消除通过迭代所有隐藏变量，在移动到下一个隐藏变量之前对单个隐藏变量执行合并和消除操作，从而交替进行合并和消除。）
+4. 你需要处理一个特殊情况，即你合并后的因子只有一个非条件变量（文档字符串详细说明了如何处理）。
+
+#### Q5a: DiscreteDistribution Class
+
+不幸的是，加入时间步长会使我们的图变得过于复杂，不适合使用变量消除。因此，我们将使用 HMM 的前向算法进行精确推理，并使用粒子过滤进行更快但近似的推理。
+
+在项目的其余部分，我们将使用 `inference.py` 中定义的 `DiscreteDistribution` 类来模拟信念分布和权重分布。这个类是内置Python字典类的扩展，其中键是分布中的不同离散元素，对应的值与分布赋予该元素的信念或权重成比例。本问题要求你填写该类中缺少的部分，这对后续问题至关重要（尽管本问题本身不计分）。
+
+首先，填写 `normalize` 方法，该方法将分布中的值规范化，使其总和为1，但保持值的比例不变。使用 `total` 方法找到分布中值的总和。对于空分布或所有值均为零的分布，不做任何操作。请注意，该方法直接修改分布，而不是返回一个新分布。
+
+其次，填写 `sample` 方法，该方法从分布中抽取一个样本，其中抽取某个键的概率与其对应值成比例。假设分布非空，并且所有值不全为零。请注意，在调用此方法之前，分布不必一定是规范化的。你可能会发现Python内置的 `random.random()` 函数对于这个问题很有用。
+
+#### Q5b: Observation Probability
+
+在这个问题中，你将在 `inference.py` 中的 `InferenceModule` 基类中实现 `getObservationProb` 方法。该方法接受一个观测值（即到鬼魂距离的噪声读数）、吃豆人的位置、鬼魂的位置和鬼魂监狱的位置，并返回给定吃豆人位置和鬼魂位置的噪声距离读数的概率。换句话说，我们希望返回
+$P(\text{noisyDistance} \mid \text{pacmanPosition}, \text{ghostPosition})$
+
+距离传感器在给定吃豆人到鬼魂的真实距离情况下对距离读数具有概率分布。该分布由函数 `busters.getObservationProbability(noisyDistance, trueDistance)` 建模，该函数返回
+$P(\text{noisyDistance} \mid \text{trueDistance})$
+该函数已经为你提供。你应该使用此函数来帮助你解决问题，并使用提供的 `manhattanDistance` 函数来查找吃豆人位置和鬼魂位置之间的距离。
+
+但是，我们还需要处理监狱的特殊情况。具体来说，当我们捕获一个鬼魂并将其送到监狱位置时，我们的距离传感器确定性地返回 None，而不是其他任何值（当且仅当鬼魂在监狱中时，观测值为 None）。其一个结果是，如果鬼魂的位置是监狱位置，那么观测值为 None 的概率是1，其他任何值的概率是0。确保在你的实现中处理这种特殊情况；每当鬼魂在监狱中，以及每当观测值为 None 时，我们实际上有一套不同的规则。
+
+要测试你的代码并运行这个问题的自动评分器，请执行：
+
+```
+python autograder.py -q q5
+```
+
+#### Q6: Exact Inference Observation
+
+在这个问题中，你将在 `inference.py` 中的 `ExactInference` 类中实现 `observeUpdate` 方法，以根据吃豆人传感器的观测值正确更新代理对鬼魂位置的信念分布。你正在实现观察新证据的在线信念更新。对于这个问题，在接收到传感器读数后，`observeUpdate` 方法应更新地图上每个位置的信念。你应该遍历 `self.allPositions` 变量，其中包括所有合法位置加上特殊的监狱位置。信念表示鬼魂在特定位置的概率，并作为一个 `DiscreteDistribution` 对象存储在名为 `self.beliefs` 的字段中，你需要更新它。
+
+在编写代码之前，写下你要解决的推理问题的方程。你应该使用你在上一个问题中编写的 `self.getObservationProb` 函数，该函数返回给定吃豆人位置、潜在鬼魂位置和监狱位置的观测概率。你可以使用 `gameState.getPacmanPosition()` 获取吃豆人的位置，使用 `self.getJailPosition()` 获取监狱位置。
+
+在吃豆人显示中，高后验信念用亮颜色表示，而低信念用暗颜色表示。你应该从一个大的信念云开始，随着更多证据的积累，逐渐缩小。在观看测试用例时，确保你理解方格是如何收敛到最终颜色的。
+
+注意：你的 `busters` 代理对他们跟踪的每个鬼魂都有一个单独的推理模块。这就是为什么即使板上有多个鬼魂，如果你在 `observeUpdate` 函数中打印一个观测值，你也只能看到一个数字。
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q6
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q6 --no-graphics
+```
+
+#### Q7: Exact Inference with Time Elapse
+
+在前一个问题中，你实现了基于吃豆人的观测进行信念更新。幸运的是，吃豆人的观测并不是他关于鬼魂可能位置的唯一信息来源。吃豆人还知道鬼魂的移动方式，即鬼魂不能穿过墙壁或在一个时间步内移动超过一个格子。
+
+为了理解这对吃豆人有何帮助，考虑以下场景：有一个吃豆人和一个鬼魂。吃豆人收到很多观测，表明鬼魂非常接近，但随后有一个观测表明鬼魂非常远。这个表明鬼魂非常远的读数很可能是一个错误的传感器导致的。吃豆人关于鬼魂移动方式的先验知识将减少这个读数的影响，因为吃豆人知道鬼魂不可能在一次移动中移动那么远。
+
+在这个问题中，你将在 `ExactInference` 类中实现 `elapseTime` 方法。对于这个问题，时间步的流逝应该更新地图上每个位置的信念。你的代理可以通过 `self.getPositionDistribution` 获取鬼魂的行动分布。为了获取给定其先前位置的鬼魂的新位置分布，使用以下代码行：
+
+```
+newPosDist = self.getPositionDistribution(gameState, oldPos)
+```
+
+其中 `oldPos` 指的是鬼魂之前的位置。`newPosDist` 是一个 `DiscreteDistribution` 对象，对于 `self.allPositions` 中的每个位置 `p`，`newPosDist[p]` 表示在时间 `t + 1` 时，鬼魂在位置 `p` 的概率，前提是鬼魂在时间 `t` 时位于位置 `oldPos`。请注意，这个调用可能相当耗时，所以如果你的代码超时，可以考虑是否可以减少对 `self.getPositionDistribution` 的调用次数。
+
+在编写任何代码之前，写下你要解决的推理问题的方程。为了单独测试你的预测实现与前一个问题中的更新实现，这个问题不会使用你的更新实现。
+
+由于吃豆人没有观测到鬼魂的行动，这些行动不会影响吃豆人的信念。随着时间的推移，吃豆人的信念将反映他认为鬼魂最可能出现的位置，这些位置是根据棋盘的几何结构和鬼魂的合法移动推测的，而吃豆人已经知道这些信息。
+
+在这个问题的测试中，我们有时会使用一个随机移动的鬼魂，有时会使用 `GoSouthGhost`。这个鬼魂倾向于向南移动，因此随着时间的推移，在没有任何观测的情况下，吃豆人的信念分布应该开始集中在棋盘的底部。要查看每个测试用例使用的鬼魂，可以查看 `.test` 文件。
+
+下图显示了贝叶斯网络/隐马尔可夫模型中发生的情况。然而，你应该依赖上面的描述来进行实现，因为某些部分已经为你实现（即 `getPositionDistribution` 被抽象为
+$ P(G_{t+1} \mid gameState, G_t) $）。
+
+![](https://inst.eecs.berkeley.edu/~cs188/sp24/assets/projects/busters_hmm_time_elapse.png)
+
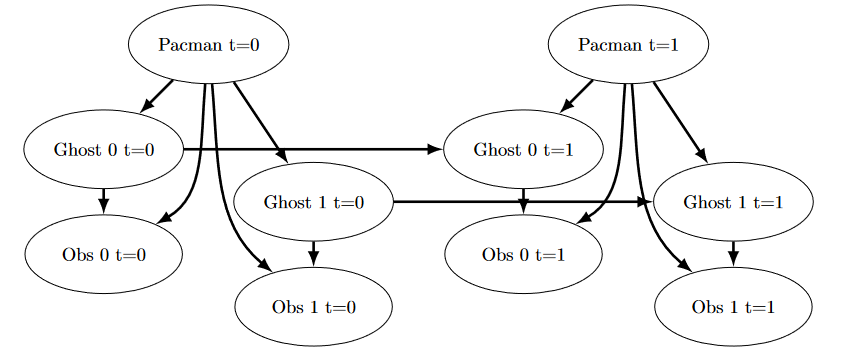
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q7
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q7 --no-graphics
+```
+
+在观看自动评分器输出时，请记住，较亮的方格表示吃豆人认为鬼魂更有可能占据该位置，而较暗的方格表示鬼魂不太可能占据该位置。对于哪些测试用例，你注意到方格的阴影出现差异？你能解释为什么一些方格变亮而一些方格变暗吗？
+
+#### Q8: Exact Inference Full Test
+
+现在，吃豆人知道如何在确定鬼魂位置时利用他的先验知识和观测，他准备自己去追捕鬼魂。我们将结合使用你的 `observeUpdate` 和 `elapseTime` 实现来保持更新的信念分布，并且你的简单贪婪代理将在每个时间步基于最新的分布选择一个行动。在简单的贪婪策略中，吃豆人假设每个鬼魂都在他认为的最可能的位置，然后朝最近的鬼魂移动。到目前为止，吃豆人是通过随机选择一个有效动作来移动的。
+
+在 `bustersAgents.py` 中实现 `GreedyBustersAgent` 的 `chooseAction` 方法。你的代理应首先找到每个尚未被捕获的鬼魂的最可能位置，然后选择一个最小化到最近鬼魂的迷宫距离的动作。
+
+要查找任意两个位置 `pos1` 和 `pos2` 之间的迷宫距离，请使用 `self.distancer.getDistance(pos1, pos2)`。要查找一个位置在执行一个动作后的后继位置：
+
+```
+successorPosition = Actions.getSuccessor(position, action)
+```
+
+你提供了 `livingGhostPositionDistributions`，这是一个 `DiscreteDistribution` 对象的列表，代表每个尚未被捕获的鬼魂的位置信念分布。
+
+如果实现正确，你的代理应该在 `q8/3-gameScoreTest` 中以至少8次超过700分的成绩赢得10次游戏中的游戏。注意：自动评分器也将直接检查你的推理的正确性，但游戏结果是一个合理的健全性检查。
+
+我们可以通过对前面的图进行如下修改来表示我们的贪婪代理的工作原理：
+
+![](https://inst.eecs.berkeley.edu/~cs188/sp24/assets/projects/busters_greedy_pacman.png)
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q8
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q8 --no-graphics
+```
+
+#### Q9: Approximate Inference Initialization and Beliefs
+
+近来，近似推理在鬼魂猎人中非常流行。在接下来的几个问题中，你将实现一个用于追踪单个鬼魂的粒子滤波算法。
+
+首先，在 `inference.py` 中的 `ParticleFilter` 类中实现 `initializeUniformly` 和 `getBeliefDistribution` 函数。在这个推理问题中，一个粒子（样本）是一个鬼魂的位置。注意，对于初始化，粒子应该均匀（而不是随机）分布在合法位置上，以确保均匀的先验分布。我们建议考虑如何使用模运算符来实现 `initializeUniformly`。
+
+请注意，你存储粒子的变量必须是一个列表。列表只是一组无权重的变量（在这种情况下是位置）。将粒子存储为任何其他数据类型（如字典）是不正确的，会产生错误。然后，`getBeliefDistribution` 方法将粒子列表转换为一个 `DiscreteDistribution` 对象。
+
+要测试你的代码并运行这个问题的自动评分器，请执行：
+
+```
+python autograder.py -q q9
+```
+
+#### Q10: Approximate Inference Observation
+
+接下来，我们将在 `inference.py` 中的 `ParticleFilter` 类中实现 `observeUpdate` 方法。该方法在 `self.particles` 上构建一个权重分布，其中一个粒子的权重是给定吃豆人位置和该粒子位置的观测概率。然后，我们从这个加权分布中重新采样以构建我们的新粒子列表。
+
+你应该再次使用 `self.getObservationProb` 函数来找到给定吃豆人位置、潜在鬼魂位置和监狱位置的观测概率。`DiscreteDistribution` 类的 `sample` 方法也将很有用。提醒一下，你可以使用 `gameState.getPacmanPosition()` 获取吃豆人的位置，使用 `self.getJailPosition()` 获取监狱位置。
+
+正确的实现必须处理一个特殊情况。当所有粒子都获得零权重时，应通过调用 `initializeUniformly` 重新初始化粒子列表。`DiscreteDistribution` 的 `total` 方法可能会有用。
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```
+python autograder.py -q q10
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```
+python autograder.py -q q10 --no-graphics
+```
+
+#### Q11: Approximate Inference with Time Elapse
+
+在 `inference.py` 中的 `ParticleFilter` 类中实现 `elapseTime` 函数。该函数应构建一个新的粒子列表，该列表对应于 `self.particles` 中的每个现有粒子前进一个时间步，然后将这个新列表分配回 `self.particles`。完成后，你应该能够像精确推理一样有效地追踪鬼魂。
+
+请注意，在这个问题中，我们将分别测试 `elapseTime` 函数，以及结合 `elapseTime` 和 `observe` 的粒子滤波器的完整实现。
+
+如同 `ExactInference` 类中的 `elapseTime` 方法一样，你应该使用：
+
+```python
+newPosDist = self.getPositionDistribution(gameState, oldPos)
+```
+
+这行代码获取给定鬼魂先前位置（`oldPos`）的新位置分布。`DiscreteDistribution` 类的 `sample` 方法也将很有用。
+
+要运行这个问题的自动评分器并可视化输出，请执行：
+
+```python
+python autograder.py -q q11
+```
+
+如果你想在没有图形的情况下运行这个测试（或任何其他测试），你可以添加以下标志：
+
+```python
+python autograder.py -q q11 --no-graphics
+```
+
+请注意，即使没有图形，这个测试也可能需要几分钟才能运行完毕。