fix: p3
This commit is contained in:
@ -19,6 +19,7 @@
|
||||
#### The Expr Class
|
||||
|
||||
在本项目的第一部分,你将使用 `logic.py` 中定义的 `Expr` 类来构建命题逻辑句子。一个 `Expr` 对象被实现为一棵树,每个节点是逻辑运算符 $(\vee, \wedge, \neg, \to, \leftrightarrow )$ ,叶子节点是文字(A, B, C, D)。以下是一个句子及其表示的示例:
|
||||
|
||||
$$
|
||||
(A \wedge B) \leftrightarrow (\neg C \vee D)
|
||||
$$
|
||||
@ -158,28 +159,28 @@ python autograder.py -q q2
|
||||
- 可能为空:你将使用这些来调用函数。
|
||||
- `walls_grid`: 仅传递给 `successorAxioms`,描述(已知的)墙。
|
||||
- `sensorModel(t: int, non_outer_wall_coords) -> Expr` 返回一个描述观测规则的单一 `Expr`;你可以查看 `sensorAxioms` 和 `SLAMSensorAxioms` 以了解示例。
|
||||
- `successorAxioms(t: int, walls_grid, non_outer_wall_coords) -> Expr` 描述过渡规则,例如 Pacman 的先前位置和动作如何影响当前的位置;我们在 `pacmanSuccessorAxiomSingle` 中见过这个。
|
||||
- `successorAxioms(t: int, walls_grid, non_outer_wall_coords) -> Expr` 描述转移规则,例如 Pacman 的先前位置和动作如何影响当前的位置;前面实现的 `pacmanSuccessorAxiomSingle` 即是如此。
|
||||
- 算法:
|
||||
- 对于 `all_coords` 中的所有 $(x, y)$,附加以下蕴涵(if-then 形式):如果 $(x, y)$ 处有一堵墙,那么 Pacman 在 $t$ 时间不在 $(x, y)$。
|
||||
- 对于 `all_coords` 中的所有 $(x, y)$,附加以下含意(if-then 形式):如果 $(x, y)$ 处有一堵墙,那么 Pacman 在 $t$ 时间不在 $(x, y)$。
|
||||
- 在时间 $t$,Pacman 恰好位于 `non_outer_wall_coords` 的一个位置。
|
||||
- 在时间 $t$,Pacman 恰好执行 `DIRECTIONS` 中的一个动作。
|
||||
- 传感器:附加上调用 `sensorAxioms` 的结果。除了 `checkLocationSatisfiability` 之外的所有调用者都使用这个;如何处理不希望添加任何传感器公理的情况由你决定。
|
||||
- 过渡:附加上调用 `successorAxioms` 的结果。所有调用者都会使用这个。
|
||||
- 传感器:附加上调用 `sensorAxioms` 的结果。除了 `checkLocationSatisfiability` 之外的所有调用者都使用这个。
|
||||
- 转移:附加上调用 `successorAxioms` 的结果。所有调用者都会使用这个。
|
||||
- 将上述每个句子添加到 `pacphysics_sentences`。如返回语句所示,这些句子将被合取并返回。
|
||||
|
||||
3. **`checkLocationSatisfiability`**:
|
||||
- 给定一个过渡 `(x0_y0,action0,x1_y1)`,`action1` 和一个问题(`problem`),编写一个函数返回一个包含两个模型的元组`(model1,model2)`:
|
||||
- 给定一个转移 `(x0_y0,action0,x1_y1)`,`action1` 和一个问题(`problem`),编写一个函数返回一个包含两个模型的元组`(model1,model2)`:
|
||||
- 在 `model1` 中,给定 `x0_y0`,`action0`,`action1`,Pacman 在 $t=1$ 时位于 $(x1, y1)$。这个模型证明 Pacman 可能在那里。如果 `model1` 为 False,我们知道 Pacman 肯定不在那里。
|
||||
- 在 `model2` 中,给定 `x0_y0`,`action0`,`action1`,Pacman 在 $t=1$ 时不在 $(x1, y1)$。这个模型证明 Pacman 可能不在那里。如果 `model2` 为 `False`,我们知道 Pacman 肯定在那里。
|
||||
- `action1` 对确定 Pacman 是否在位置上没有影响;它只是在使你的解决方案与自动评分器解决方案匹配。
|
||||
- 要实现这个问题,你需要向你的 KB 添加以下表达式:
|
||||
- 向 KB 添加:`pacphysics_axioms(...)`,以及适当的时间。没有 `sensorModel`,因为我们知道吃豆人世界上的一切。需要时,使用 `allLegalSuccessorAxioms` 进行过渡,因为这是针对常规 Pacman 过渡规则。
|
||||
- 向 KB 添加:`pacphysics_axioms(...)`,以及适当的时间。没有 `sensorModel`,因为我们知道吃豆人世界上的一切。需要时,使用 `allLegalSuccessorAxioms` 进行转移,这是针对常规 Pacman 的转移规则。
|
||||
- 向 KB 添加:Pacman 的当前位置 $(x0, y0)$
|
||||
- 向 KB 添加:Pacman 执行 `action0`
|
||||
- 向 KB 添加:Pacman 执行 `action1`
|
||||
- 使用 `findModel` 对上述两个模型进行查询。查询应该是不同的;关于如何进行查询,请参见 `entails`。
|
||||
|
||||
提醒:表示 Pacman 在时间 $t$ 位于 $(x, y)$ 的变量是 `PropSymbolExpr(pacman_str, x, y, time=t)`,表示 $(x, y)$ 处有墙的是 `PropSymbolExpr(wall_str, x, y)`,表示在 $t$ 时间执行动作 `action` 的是 `PropSymbolExpr(action, time=t)`。
|
||||
提示:表示 Pacman 在时间 $t$ 位于 $(x, y)$ 的变量是 `PropSymbolExpr(pacman_str, x, y, time=t)`,表示 $(x, y)$ 处有墙的是 `PropSymbolExpr(wall_str, x, y)`,表示在 $t$ 时间执行动作 `action` 的是 `PropSymbolExpr(action, time=t)`。
|
||||
|
||||
要测试和调试你的代码,请运行:
|
||||
|
||||
@ -195,23 +196,19 @@ Pacman 正试图找到迷宫的终点(目标位置)。使用命题逻辑实
|
||||
|
||||
**`positionLogicPlan(problem)`**:给定一个 `logicPlan.PlanningProblem` 的实例,返回 Pacman 执行的一系列动作字符串。
|
||||
|
||||
你不会实现搜索算法,而是创建代表所有可能位置在每个时间处的 `pacphysics` 的表达式。这意味着在每个时间,你应该为网格上的所有可能位置添加通用规则,这些规则不假设 Pacman 的当前位置。
|
||||
你不需要实现搜索算法,而是创建代表所有可能位置在每个时间处的 `pacphysics` 的表达式。这意味着在每个时间,你应该为网格上的所有可能位置添加通用规则,这些规则不需要假设 Pacman 的当前位置。
|
||||
|
||||
你需要为知识库编写以下句子,形式如下:
|
||||
|
||||
- **添加到知识库**:
|
||||
- 初始知识:时间 0 时Pacman的初始位置。
|
||||
- **初始**:时间 0 时Pacman的初始位置。
|
||||
|
||||
- **循环(时间范围为 50,因为自动评分器不会测试需要 ≥50 时间的布局)**:
|
||||
- 打印时间:查看代码运行情况以及运行到何处。
|
||||
- 初始知识:时间 $t$ 时,Pacman 只能在 `non_wall_coords` 中的一个(`exactlyOne`)位置。这类似于 `pacphysicsAxioms`,但不要使用该方法,因为在生成可能位置列表时我们使用的是 `non_wall_coords`(稍后使用 `walls_grid`)。
|
||||
- 时间 $t$ 时,Pacman 只能在 `non_wall_coords` 中的一个(`exactlyOne`)位置。这类似于 `pacphysicsAxioms`,但不要使用该方法,因为在生成可能位置列表时我们使用的是 `non_wall_coords`(稍后使用 `walls_grid`)。
|
||||
- 知识库中现有变量是否存在满足赋值?使用 `findModel` 并传入目标断言和知识库。
|
||||
- 如果存在,使用 `extractActionSequence` 从起点到目标返回一系列动作。
|
||||
- 目标断言是在时间 $t$ 时 Pacman 位于目标的位置的表达式。
|
||||
|
||||
- **添加到知识库**:
|
||||
- 如果存在,使用 `extractActionSequence` 从起点到目标返回一系列动作。
|
||||
- Pacman 每个时间执行一个动作。
|
||||
- 过渡模型句子:为 `non_wall_coords` 中所有可能的 Pacman 位置调用 `pacmanSuccessorAxiomSingle(...)`。
|
||||
- 转移模型句子:为 `non_wall_coords` 中所有可能的 Pacman 位置调用 `pacmanSuccessorAxiomSingle(...)`。
|
||||
|
||||
|
||||
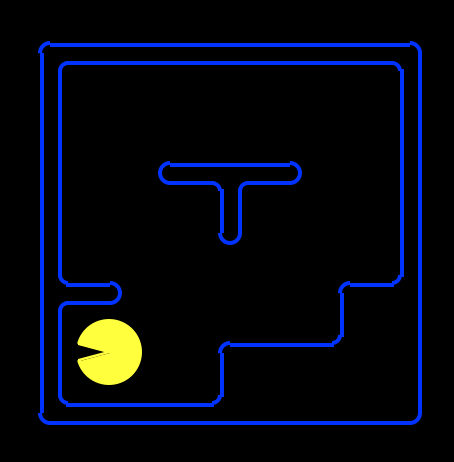
请注意,根据我们设置 Pacman 网格的方式,Pacman 可占据的最左下角的空间(假设那里没有墙)是 $(1,1)$,而不是 $(0,0)$,如下所示。
|
||||
@ -219,10 +216,10 @@ Pacman 正试图找到迷宫的终点(目标位置)。使用命题逻辑实
|
||||
|
||||
|
||||
Pacphysics 在 Q3 和 Q4 中的总结(也见于AIMA第7.7章):
|
||||
- 对于所有 $x, y, t$:如果 $(x, y)$ 处有墙,则Pacman在 $t$ 时间不在 $(x, y)$。
|
||||
- 对于每个 $t$:Pacman恰好在所有可能的 $(x, y)$ 位置之一。可以通过外部或所有墙的知识进行优化,按照每个函数的规范。
|
||||
- 对于每个 $t$:Pacman恰好执行一个可能的动作。
|
||||
- 对于每个 $t$(除 $t = ??$ 外):过渡模型:Pacman在 $t$ 时间在 $(x, y)$ 当且仅当他在 $t-1$ 时间在 $(x-dx, y-dy)$ 并在 $t-1$ 时间执行了 $(dx, dy)$ 动作。
|
||||
- 对于所有 $x, y, t$:如果 $(x, y)$ 处有墙,则 Pacman 在 $t$ 时间不在 $(x, y)$。
|
||||
- 对于每个 $t$:Pacman 恰好在所有可能的 $(x, y)$ 位置之一。
|
||||
- 对于每个 $t$:Pacman 恰好执行一个可能的动作。
|
||||
- 对于每个 $t$(除 $t = ??$ 外):转移模型:Pacman在 $t$ 时间在 $(x, y)$ 当且仅当他在 $t-1$ 时间在 $(x-dx, y-dy)$ 并在 $t-1$ 时间执行了 $(dx, dy)$ 动作。
|
||||
|
||||
在较小的迷宫上测试代码:
|
||||
|
||||
@ -241,7 +238,7 @@ python autograder.py -q q4
|
||||
### 调试提示:
|
||||
|
||||
- 如果你发现解决方案长度为 0 或 1:仅仅知道Pacman在给定时间的位置是否足够?是什么阻止他同时出现在其他地方?
|
||||
- 作为理智检查,验证如果Pacman在时间 $0$ 在 $(1,1)$,并在时间 $6$ 在 $(4,4)$,他在此期间从未在 $(5,5)$。
|
||||
- 作为 sanity check,验证如果Pacman在时间 $0$ 在 $(1,1)$,并在时间 $6$ 在 $(4,4)$,他在此期间从未在 $(5,5)$。
|
||||
- 如果解决方案运行时间超过几分钟,你可能需要重新审视 exactlyOne 和 atMostOne 的实现,并确保使用尽可能少的子句。
|
||||
|
||||
#### Q5: Eating All the Food
|
||||
@ -250,13 +247,13 @@ Pacman 试图吃掉棋盘上的所有食物。使用命题逻辑实现以下方
|
||||
|
||||
**`foodLogicPlan(problem)`**:给定一个 `logicPlan.PlanningProblem` 实例,返回 Pacman 执行的一系列动作字符串。
|
||||
|
||||
这个问题的总体格式与问题 4 相同;你可以从那里复制你的代码作为起点。问题 4 的注释和提示也适用于这个问题。你需要实现以前问题中未实现的所有必要的后继状态公理。
|
||||
这个问题的总体格式与问题 4 相同;你可以从那里复制你的代码作为起点。问题 4 的注释和提示也适用于这个问题。
|
||||
|
||||
**与前一问题的变化:**
|
||||
|
||||
- 初始化 `Food[x,y]_t` 变量,根据初始信息使用代码 `PropSymbolExpr(food_str, x, y, time=t)`,当且仅当 $ t $ 时间 $(x, y)$ 处有食物时,每个变量为真。
|
||||
- 改变目标断言:你的目标断言句子必须在且仅在所有食物都被吃掉时为真。当所有 `Food[x,y]_t` 为假时发生。
|
||||
- 添加食物后继公理:`Food[x,y]_t+1` 和 `Food[x,y]_t` 以及 `Pacman[x,y]_t` 之间的关系是什么?食物后继公理只应涉及这三个变量,对于任何给定的 $(x, y)$ 和 $t$。考虑食物变量的过渡模型,并在每个时间步将这些句子添加到你的知识库中。
|
||||
- 初始化 `Food[x,y]_t` 变量,根据初始信息使用代码 `PropSymbolExpr(food_str, x, y, time=t)`,当且仅当 $t$ 时间 $(x, y)$ 处有食物时,每个变量为真。
|
||||
- 改变目标断言:你的目标断言句子必须在且仅在所有食物都被吃掉时为真。也就是当所有 `Food[x,y]_t` 为假时,其为真。
|
||||
- 添加食物后继公理:`Food[x,y]_t+1` 和 `Food[x,y]_t` 以及 `Pacman[x,y]_t` 之间的关系是什么?食物后继公理只应涉及这三个变量,对于任何给定的 $(x, y)$ 和 $t$。考虑食物变量的转移模型,并在每个时间将这些句子添加到你的知识库中。
|
||||
|
||||
测试代码:
|
||||
|
||||
@ -264,7 +261,7 @@ Pacman 试图吃掉棋盘上的所有食物。使用命题逻辑实现以下方
|
||||
python pacman.py -l testSearch -p LogicAgent -a fn=flp,prob=FoodPlanningProblem
|
||||
```
|
||||
|
||||
我们不会在需要超过 50 个时间的布局上测试你的代码。
|
||||
我们的测试不会在需要超过 50 个时间的布局上。
|
||||
|
||||
测试和调试代码:
|
||||
|
||||
@ -274,12 +271,12 @@ python autograder.py -q q5
|
||||
|
||||
#### 其余项目的辅助函数
|
||||
|
||||
对于剩下的问题,我们将依赖以下辅助函数,这些函数将在定位、建图和SLAM的伪代码中引用。
|
||||
对于剩下的问题,我们将依赖以下辅助函数,这些函数将在定位、建图和 SLAM 的伪代码(算法)中引用。
|
||||
|
||||
##### 将 pacphysics、动作和感知信息添加到 KB:
|
||||
- 添加到 KB:`pacphysics_axioms(...)`(你在Q3中编写的)。使用 `sensorAxioms` 和 `allLegalSuccessorAxioms` 进行定位和建图,只在 SLAM 中使用 `SLAMSensorAxioms` 和 `SLAMSuccessorAxioms`。
|
||||
- 添加到 KB:Pacman 采取由 `agent.actions[t]` 规定的动作。
|
||||
- 通过调用 `agent.getPercepts()` 获取感知并将感知传递给 `fourBitPerceptRules(...)` 以进行定位和建图,或传递给 `numAdjWallsPerceptRules(...)` 以进行SLAM。将生成的 `percept_rules` 添加到 KB。
|
||||
- 通过调用 `agent.getPercepts()` 获取感知并将感知传递给 `fourBitPerceptRules(...)` 以进行定位和建图,或传递给 `numAdjWallsPerceptRules(...)` 以进行 SLAM。将生成的 `percept_rules` 添加到 KB。
|
||||
|
||||
##### 使用更新的 KB 查找可能的 Pacman 位置:
|
||||
- `possible_locations = []`
|
||||
@ -288,16 +285,16 @@ python autograder.py -q q5
|
||||
- 如果存在满足赋值的情况,在时间 $t$ Pacman 在 $(x, y)$,则将 $(x, y)$ 添加到 `possible_locations`。
|
||||
- 添加到 KB:在时间 $t$ Pacman 明确在的位置 $(x, y)$。
|
||||
- 添加到 KB:在时间 $t$ Pacman 明确不在的位置 $(x, y)$。
|
||||
- 提示:检查 `entails` 的结果是否相互矛盾(即 KB `entails A` 和 `entails ¬A`)。如果是,打印反馈以帮助调试。
|
||||
- 提示:检查 `entails` 的结果是否相互矛盾(即 KB `entails` $A$ 和 `entails` $\neg A$)。如果是,打印反馈以帮助调试。
|
||||
|
||||
##### 使用更新的 KB 查找可证明的墙位置:
|
||||
- 遍历 `non_outer_wall_coords`。
|
||||
- 我们能否证明 $(x, y)$ 处有墙?我们能否证明 $(x, y)$ 处没有墙?使用 `entails` 和 KB。
|
||||
- 添加到 KB 并更新 `known_map`:明确有墙的位置 $(x, y)$。
|
||||
- 添加到 KB 并更新 `known_map`:明确没有墙的位置 $(x, y)$。
|
||||
- 提示:检查 `entails` 的结果是否相互矛盾(即 KB `entails A` 和 `entails ¬A`)。如果是,打印反馈以帮助调试。
|
||||
- 提示:检查 `entails` 的结果是否相互矛盾(即 KB `entails` $A$ 和 `entails` $\neg A$)。如果是,打印反馈以帮助调试。
|
||||
|
||||
**观察**:我们将已知的 Pacman 位置和墙添加到 KB,以便在后续时间步中不必重新查找这些内容;从技术上讲,这是冗余信息,因为我们首先使用 KB 证明了这一点。
|
||||
**观察**:我们把已知的 Pacman 位置和墙的位置添加到知识库中,这样在后续的时间步中,就不需要重新计算这些信息了。虽然从技术上讲,这些信息是冗余的,因为我们已经用知识库证明了这些信息,但是这样做可以简化后续计算,提高效率。
|
||||
|
||||
#### Q6: Localization
|
||||
|
||||
@ -305,11 +302,11 @@ Pacman 从已知地图开始,但起始位置未知。它有一个 4-bit 的传
|
||||
|
||||
**`localization(problem, agent)`**:给 定 `logicPlan.LocalizationProblem` 的一个实例和 `logicAgents.LocalizationLogicAgent` 的一个实例,在时间 0 到 `agent.num_steps-1` 之间重复生成在时间 $t$ 可能的位置列表 $(x_i, y_i)$:`[ (x_0_0, y_0_0), (x_1_0, y_1_0), ...]`。注意,你不需要担心生成器的工作方式,因为这行代码已经为你写好了。
|
||||
|
||||
为了让 Pacman 在定位过程中使用传感器信息,你将使用已经为你实现的两个方法。`sensorAxioms`, 即 $Blocked[Direction]_t \leftrightarrow [(P[x_i,y_j]_t\wedge WALL[x_i+dx,y_j+dy])\vee (P[x_i',y_j']_t\wedge WALL[x_i'+dx,y_j'+dy])...]$ 和 `fourBitPerceptRules`,它们将时间t的感知转换为逻辑句子。
|
||||
为了让 Pacman 在定位过程中使用传感器信息,你将使用已经为你实现的两个方法。`sensorAxioms`, 即 $Blocked[Direction]_t \leftrightarrow [(P[x_i,y_j]_t\wedge WALL[x_i+dx,y_j+dy])\vee (P[x_i',y_j']_t\wedge WALL[x_i'+dx,y_j'+dy])...]$ 和 `fourBitPerceptRules`,它们将时间 $t$ 的感知转换为逻辑句子。
|
||||
|
||||
请按照我们的伪代码实现该函数:
|
||||
|
||||
- **添加到知识库**:墙所在的位置(walls_list)和不在的位置(not in walls_list)。
|
||||
- **添加到知识库**:墙所在的位置(`walls_list`)和不在的位置(not in `walls_list`)。
|
||||
- **对于在 `range(agent.num_timesteps)` 中的 $t$**:
|
||||
- 添加 pacphysics、动作和感知信息到知识库。
|
||||
- 使用更新的知识库查找可能的 Pacman 位置。
|
||||
@ -350,7 +347,10 @@ Pacman 现在知道了他的起始位置,但不知道墙的位置(除了外
|
||||
python autograder.py -q q7
|
||||
```
|
||||
|
||||
#### Q8: Simultaneous Localization and Mapping (SLAM)
|
||||
|
||||
有时,Pacman 在迷失和黑暗中徘徊。
|
||||
|
||||
在 SLAM(同时定位与建图)中,Pacman 知道他的初始坐标,但不知道墙的位置。在 SLAM 中,Pacman 可能会无意中采取非法动作(例如,当北面有墙阻挡时向北走),这会增加 Pacman 随时间的不确定性。此外,在我们的 SLAM 设置中,Pacman 不再有一个4位的传感器来告诉我们四个方向是否有墙,而是只有一个 3-bit 的传感器,揭示他附近有多少墙。这有点像 WiFi 信号强度条;000 表示没有邻近的墙,100 表示恰好有1面墙相邻,110 表示恰好有2面墙相邻,111 表示恰好有3面墙相邻。这 3 位由 3 个布尔值的列表表示。因此,你将使用 `SLAMSensorAxioms` 和 `numAdjWallsPerceptRules`,而不是 `sensorAxioms` 和 `fourBitPerceptRules`。你将编写帮助 Pacman 确定以下内容的句子:(1)每个时间的可能位置,(2)墙的位置,具体实现方法如下:
|
||||
|
||||
**slam(problem, agent)**:给定一个 `logicPlan.SLAMProblem` 和 `logicAgents.SLAMLogicAgent` 的实例,重复生成一个包含两个项目的元组:
|
||||
|
||||
Reference in New Issue
Block a user