3.0 KiB
3.0 KiB
贝叶斯网络
介绍
贝叶斯网络是一种概率图式模型,通过对随机变量构建有向无环图捕捉其概率分布。更具体地,你的任务为通过条件概率表来完成指定的查询,即给定先验概率 P(Q) 和条件概率 P(E|Q), 求解后验概率 P(Q|e). 为了解决这一问题,我们可以构建联合分布
P(EQ) = P(E|Q) P(Q)
再计算
P(Q|e) = \frac{P(Qe)}{P(e)} = \frac{P(Qe)}{\sum_{q} P(qe)}
这样就可以通过联合概率分布来计算后验概率。这一实现存在两个很大的问题:
- 完整的联合分布概率表的大小与事件个数呈指数关系(为什么?),导致存储与计算开销太大。
- 先验地估计所有信息是困难的。
为此我们考察使用条件概率分布进行推理,即使用贝叶斯公式:
P(Q|e) = \frac{P(e|Q) P(Q)}{\sum_{q} P(e|q) P(q)}
这是贝叶斯网络背后的动机:一种使用简单的局部分布(条件概率)描述复杂联合分布(模型)的技术。我们描述变量如何在局部相互作用,并将这些作用组合建模全局的间接相互作用。
栗子
在使用 Google 搜索时,当你不小心输入一个不存在的单词时,搜索引擎会提示你是不是要输入某一个正确的单词。Google的拼写检查基于贝叶斯方法。下面我们就来看看,怎么利用贝叶斯方法,实现"拼写检查"的功能。
用户输入一个单词时,可能拼写正确,也可能拼写错误。如果把拼写正确的情况记做c(代表correct),拼写错误的情况记做 w(代表wrong),那么“拼写检查”要做的事情就是:在发生 w 的情况下,试图推断出 c。换言之,已知w,然后在若干个备选方案中,找出可能性最大的那个 c, 也就是求 P(c|w)=P(w|c)P(c)/P(w) 的最大值,故只需考察 \operatorname{argmax}_{c} P(w|c)P(c) 即可。
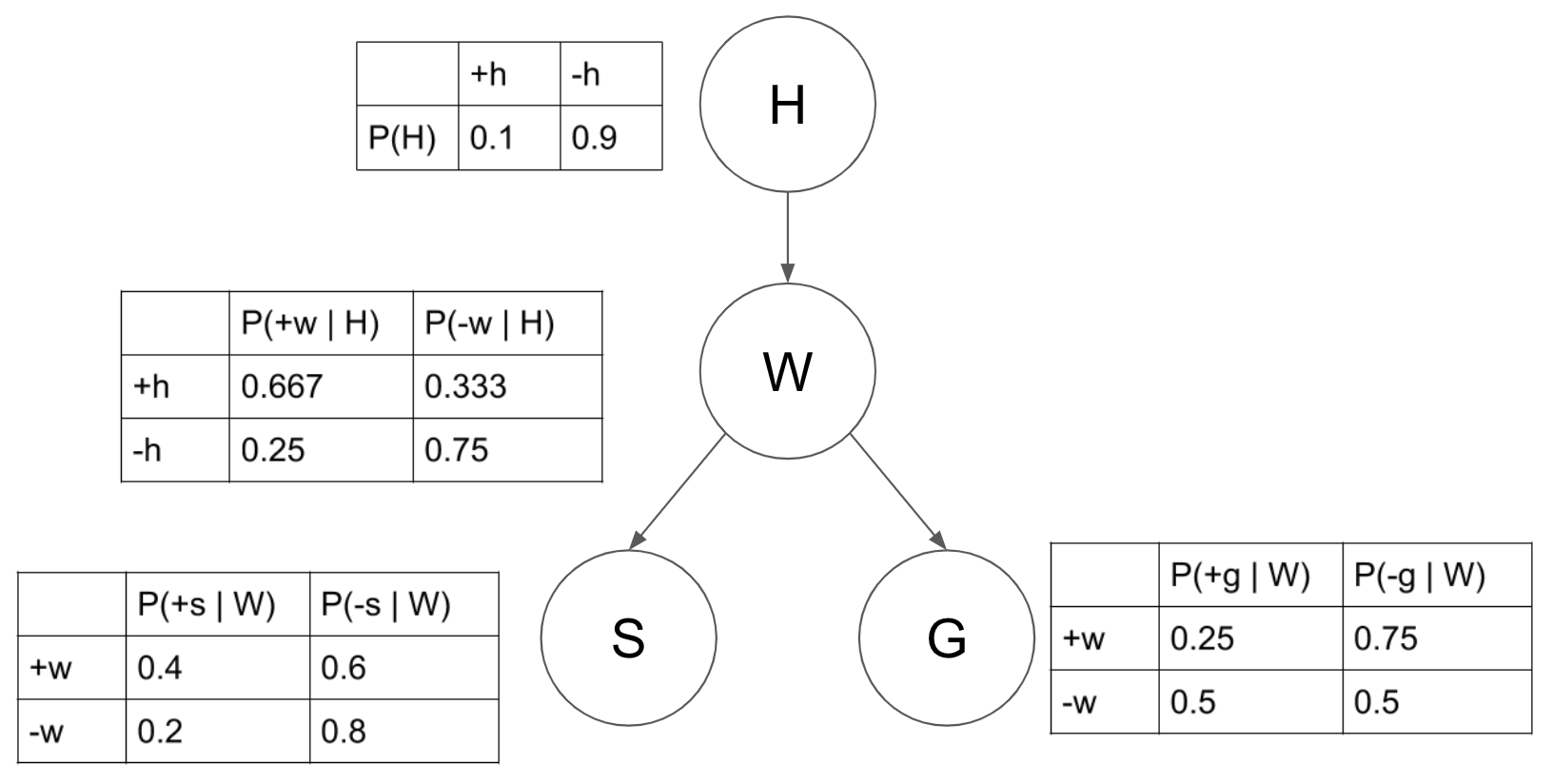
上面是一个实际的贝叶斯网络的例子,其中每个节点代表一个事件,节点对应的表即为贝叶斯网络中存储的信息,若我们想要计算 $ P(+w \mid +s, -g) $,则有:
P(+w \mid +s, -g) = \frac{P(+w, +s, -g)}{P(+s, -g)}
(链式规则)
P(+w, +s, -g) = \sum_h P(h, +w, +s, -g)
(边缘化)
\sum_{h, w} P(h, w, +s, -g) = \sum_h P(h)P(+w \mid h)P(+s \mid +w)P(-g \mid +w)
(联合概率分布 = 边缘概率分布的乘积)
\begin{aligned}
P(+w \mid +s, -g) &= \frac{P(+w, +s, -g)}{P(+s, -g)} \quad (\text{条件概率}) \\
&= \frac{\sum_h P(h, +w, +s, -g)}{\sum_{h, w} P(h, w, +s, -g)} \quad (\text{联合分布转边缘分布}) \\
&= \frac{\sum_h P(h)P(+w \mid h)P(+s \mid +w)P(-g \mid +w)}{\sum_{h,w} P(h)P(w
\mid h)P(+s \mid w)P(-g \mid w)} \quad (\text{转为条件概率的乘积}) \\
&= \frac{0.1 \times 0.667 \times 0.4 \times 0.75 + 0.9 \times 0.25 \times 0.4 \times 0.75}{0.1 \times 0.667 \times 0.4 \times 0.75 + 0.9 \times 0.25 \times 0.4 \times 0.75 + 0.1 \times 0.333 \times 0.2 \times 0.5 + 0.9 \times 0.75 \times 0.2 \times 0.5} \\
&= 0.553
\end{aligned}