124 lines
7.3 KiB
Markdown
124 lines
7.3 KiB
Markdown
~~coming soon~~
|
||
|
||
#### 介绍
|
||
|
||
在这个项目中,你将编写简单的 Python 函数,生成描述 Pacman 物理状态(记为 **pacphysics**)的逻辑句子。然后,你将使用 SAT 求解器 pycosat,解决与 规划(生成动作序列以到达目标位置并吃掉所有点)、定位(根据本地传感器模型在地图中找到自己)、建图(从零开始构建地图)以及 SLAM(同时定位与建图)相关的逻辑推理任务。
|
||
|
||
你需要补全的代码文件有:
|
||
|
||
- logicPlan.py
|
||
|
||
你可以阅读并参考来帮助你实现代码的文件有:
|
||
|
||
- logic.py
|
||
- logicAgents.py:以逻辑规划形式定义了Pacman在本项目中将遇到的两个具体问题。
|
||
- game.py:Pacman世界的内部模拟器代码。你可能需要查看的是其中的Grid类。
|
||
|
||
你可以忽略其他支持文件。
|
||
|
||
#### The Expr Class
|
||
|
||
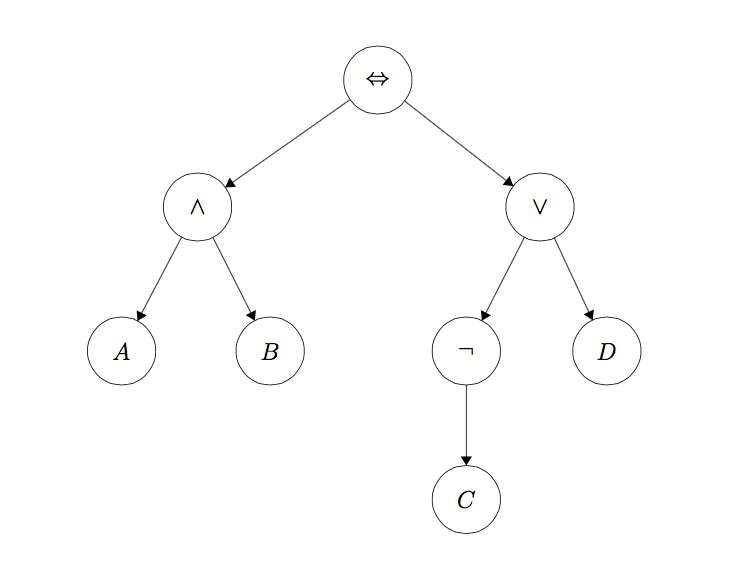
在本项目的第一部分,你将使用 `logic.py` 中定义的 `Expr` 类来构建命题逻辑句子。一个 `Expr` 对象被实现为一棵树,每个节点是逻辑运算符 $(\vee, \wedge, \neg, \to, \leftrightarrow )$ ,叶子节点是文字(A, B, C, D)。以下是一个句子及其表示的示例:
|
||
$$
|
||
(A \wedge B) \leftrightarrow (\neg C \vee D)
|
||
$$
|
||
|
||
|
||
|
||
要实例化名为 'A' 的符号,请像这样调用构造函数:
|
||
|
||
```python
|
||
A = Expr('A')
|
||
```
|
||
该 `Expr` 类允许你使用 Python 运算符来构建这些表达式。以下是可用的 Python 运算符及其含义:
|
||
|
||
- `~A`: $\neg A$
|
||
- `A & B`: $A \wedge B$
|
||
- `A | B`: $A \vee B$
|
||
- `A >> B`: $A \to B$
|
||
- `A % B`: $A \leftrightarrow B$
|
||
|
||
因此要构建表达式 $A \wedge B$,你可以这样做:
|
||
|
||
```python
|
||
A = Expr('A')
|
||
B = Expr('B')
|
||
A_and_B = A & B
|
||
```
|
||
|
||
(请注意,该示例中赋值运算符左边 `A` 只是一个 Python 变量名,即 `symbol1 = Expr('A')` 也可以正常工作。)
|
||
|
||
**关于 conjoin 和 disjoin:**
|
||
|
||
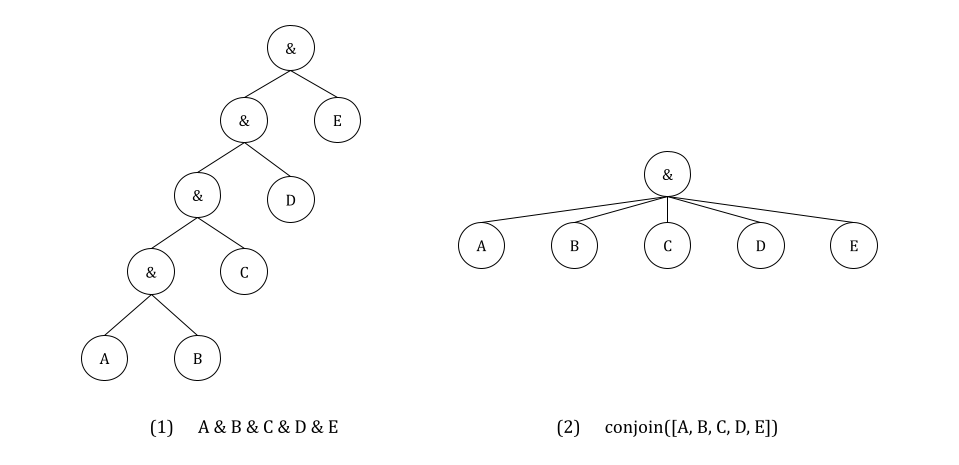
在可能的情况下,必须使用 `conjoin` 和 `disjoin` 操作符。`conjoin` 创建一个链式的 `&`(逻辑与)表达式,`disjoin` 创建一个链式的 `|`(逻辑或)表达式。假设你想检查条件 A、B、C、D 和 E 是否全部为真。简单的实现方法是写 `condition = A & B & C & D & E`,但这实际上会转换为 `((((A & B) & C) & D) & E)`,这会创建一个非常嵌套的逻辑树(见下图中的(1)),调试起来非常困难。相反,`conjoin` 可以创建一个扁平的树(见下图中的(2))。
|
||
|
||
|
||
|
||
#### 命题符号命名(重要!)
|
||
在项目的后续部分,请使用以下变量命名规则:
|
||
|
||
- 引入变量时,必须以大写字母开头(包括 `Expr`)。
|
||
- 变量名中只能出现以下字符:`A-Z`、`a-z`、`0-9`、`_`、`^`、`[`、`]`。
|
||
- 逻辑连接字符 (`&`, `|`) 不得出现在变量名中。例如,`Expr('A & B')` 是非法的,因为它试图创建一个名为 `'A & B'` 的常量符号。应使用 `Expr('A') & Expr('B')` 来创建逻辑表达式。
|
||
|
||
**Pacphysics 符号**
|
||
|
||
- `PropSymbolExpr(pacman_str, x, y, time=t)`:表示 Pacman 是否在时间 `t` 处于 (x,y),写作 `P[x,y]_t`。
|
||
- `PropSymbolExpr(wall_str, x, y)`:表示 `(x,y)` 处是否有墙,写作 `WALL[x,y]`。
|
||
- `PropSymbolExpr(action, time=t)`:表示 Pacman 是否在时间 `t` 采取 `action` 动作,其中 `action` 是 `DIRECTIONS` 的元素,例如 North_t`。
|
||
- 一般情况下,`PropSymbolExpr(str, a1, a2, a3, a4, time=a5)` 创建表达式 `str[a1,a2,a3,a4]_a5`,其中 `str` 是一个字符串。
|
||
|
||
`logic.py` 文件中有关于 `Expr` 类的更多详细文档。
|
||
|
||
#### SAT 求解器
|
||
|
||
一个SAT(可满足性)求解器接受编码世界规则的逻辑表达式,并返回一个满足该表达式的模型(逻辑符号的真值分配),如果存在这样的模型。为了高效地从表达式中找到可能的模型,我们利用 [pycosat](https://pypi.org/project/pycosat/) 模块,这是 [picoSAT](https://fmv.jku.at/picosat/) 库的Python包装器。
|
||
|
||
运行`conda install pycosat` 安装。
|
||
|
||
**测试pycosat安装**:
|
||
|
||
在 `logic` 目录下运行:
|
||
|
||
```
|
||
python pycosat_test.py
|
||
```
|
||
|
||
这应该输出:
|
||
|
||
```
|
||
[1, -2, -3, -4, 5]
|
||
```
|
||
|
||
如果你在设置过程中遇到问题,请告知我们。这对于完成项目至关重要,我们不希望你在安装过程中浪费时间。
|
||
|
||
#### Q1: Logic Warm-up
|
||
|
||
这个问题将让你练习使用项目中用于表示命题逻辑句子的 `Expr` 数据类型。你将在 `logicPlan.py` 中实现以下函数:
|
||
|
||
- `sentence1()`: 创建一个 `Expr` 实例,表示以下三个句子为真的命题。不要进行任何逻辑简化,只需按此顺序将它们放入列表中,并返回列表的合取。列表中的每个元素应该对应这三个句子中的每一个。
|
||
$$
|
||
A \vee B \\
|
||
\neg A \leftrightarrow (\neg B \vee C) \\
|
||
\neg A \vee \neg B \vee C
|
||
$$
|
||
- `sentence2()`: 创建一个Expr实例,表示以下四个句子为真的命题。同样,不要进行任何逻辑简化,只需按此顺序将它们放入列表中,并返回列表的合取。
|
||
$$
|
||
C \leftrightarrow (B \vee D) \\
|
||
A \to (\neg B \wedge \neg D) \\
|
||
\neg(B \wedge \neg C) \to A \\
|
||
\neg D \to C
|
||
$$
|
||
- `sentence3()`: 使用 `PropSymbolExpr` 构造函数,创建符号 `'PacmanAlive_0'`、`'PacmanAlive_1'`、`'PacmanBorn_0'` 和 `'PacmanKilled_0'`(提示:回忆一下 `PropSymbolExpr(str, a1, a2, a3, a4, time=a5)` 创建的表达式是 `str[a1,a2,a3,a4]_a5`,其中 `str` 是一个字符串;对于这个问题,你应该创建一些与这些字符串完全匹配的字符串)。然后,创建一个 `Expr` 实例,以命题逻辑的形式按顺序编码以下三个英文句子,而不进行任何简化:
|
||
1. 如果 Pacman 在时间 1 是活着的,当且仅当他在时间 0 是活着并且他在时间 0 没有被杀死,或者他在时间 0 不是活着的并且他在时间 0 出生。
|
||
2. 在时间 0,Pacman 不能既是活着的又出生。
|
||
3. Pacman 在时间 0 出生。
|
||
- `findModelUnderstandingCheck()`:
|
||
1. 查看 `findModel(sentence)` 方法的工作原理:它使用 `to_cnf` 将输入句子转换为合取范式(SAT求解器所需的形式),并将其传递给SAT求解器以找到满足句子(`sentence`)中符号的赋值,即一个模型。模型是一个 表达式中符号 的字典,并对应有 `True` 或 `False` 的赋值。通过打开 Python 交互会话并运行 `from logicPlan import *` 和 `findModel(sentence1())` 及其他两个类似查询来测试。它们是否与预期一致?
|
||
2. 基于上述内容,填写 `findModelUnderstandingCheck` 以便它返回 `findModel(Expr('a'))` 会返回的结果(如果允许使用小写变量)。不应使用 `findModel` 或 `Expr` 超出已有的内容;只需直接重现输出即可。
|
||
- `entails(premise, conclusion)`: 仅当前提(`premise`)蕴含结论(`conclusion`)时才返回 `True`。提示:`findModel` 在这里很有帮助;思考为了使其为真,什么必须是不可满足的,以及不可满足意味着什么。
|
||
- `plTrueInverse(assignments, inverse_statement)`: 仅当给定赋值时,(not `inverse_statement`) 为真时,才返回 True。
|
||
|
||
### 翻译:
|
||
|
||
在继续之前,尝试实例化一个小句子,例如 \(A \wedge B \rightarrow C\),并对其调用 `to_cnf`。检查输出并确保你理解它。 |