ZYM/PPCA-AIPacMan-2024
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity
Files
65c6f1c60a03ad8e2b8c37109bedbcc2aeb51cbf
PPCA-AIPacMan-2024/logic/README.md
zsq259 65c6f1c60a feat: p3
2024-06-26 16:32:08 +08:00

26 KiB
Raw Blame History

coming soon

介绍

在这个项目中，你将编写简单的 Python 函数，生成描述 Pacman 物理状态（记为 pacphysics）的逻辑句子。然后，你将使用 SAT 求解器 pycosat，解决与 规划（生成动作序列以到达目标位置并吃掉所有点）、定位（根据本地传感器模型在地图中找到自己）、建图（从零开始构建地图）以及 SLAM（同时定位与建图）相关的逻辑推理任务。

你需要补全的代码文件有：

  • logicPlan.py

你可以阅读并参考来帮助你实现代码的文件有：

  • logic.py
  • logicAgents.py：以逻辑规划形式定义了Pacman在本项目中将遇到的两个具体问题。
  • game.py：Pacman世界的内部模拟器代码。你可能需要查看的是其中的Grid类。

你可以忽略其他支持文件。

The Expr Class

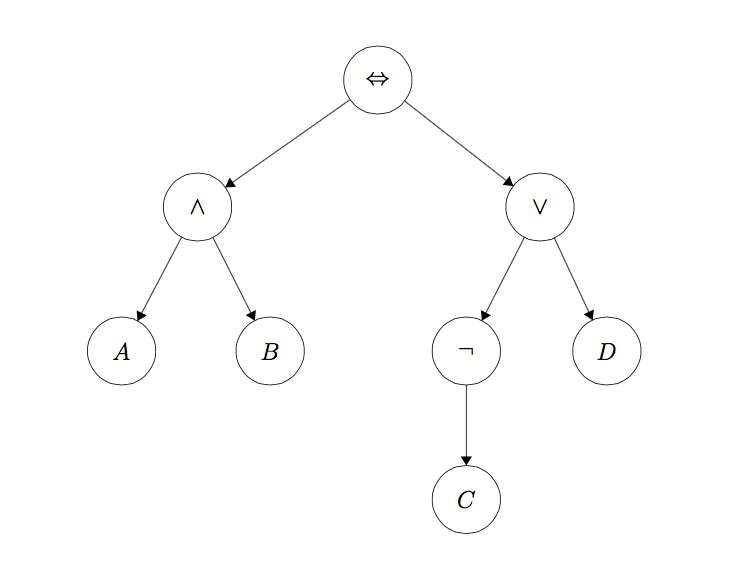
在本项目的第一部分，你将使用 logic.py 中定义的 Expr 类来构建命题逻辑句子。一个 Expr 对象被实现为一棵树，每个节点是逻辑运算符 (\vee, \wedge, \neg, \to, \leftrightarrow ) ，叶子节点是文字（A, B, C, D）。以下是一个句子及其表示的示例：


(A \wedge B) \leftrightarrow (\neg C \vee D)

要实例化名为 'A' 的符号，请像这样调用构造函数：

A = Expr('A')

该 Expr 类允许你使用 Python 运算符来构建这些表达式。以下是可用的 Python 运算符及其含义：

  • ~A: \neg A
  • A & B: A \wedge B
  • A | B: A \vee B
  • A >> B: A \to B
  • A % B: A \leftrightarrow B

因此要构建表达式 $A \wedge B$，你可以这样做：

A = Expr('A')
B = Expr('B')
A_and_B = A & B

（请注意，该示例中赋值运算符左边 A 只是一个 Python 变量名，即 symbol1 = Expr('A') 也可以正常工作。）

关于 conjoin 和 disjoin：

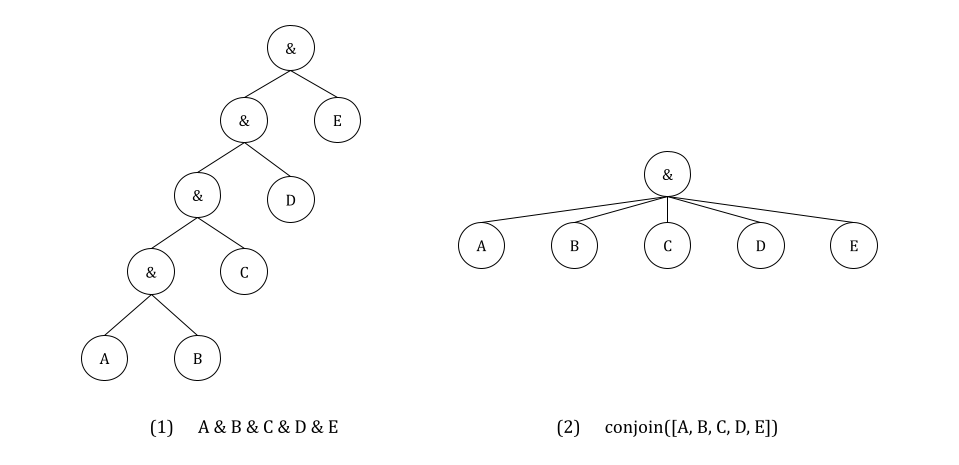
在可能的情况下，必须使用 conjoin 和 disjoin 操作符。conjoin 创建一个链式的 &（逻辑与）表达式，disjoin 创建一个链式的 |（逻辑或）表达式。假设你想检查条件 A、B、C、D 和 E 是否全部为真。简单的实现方法是写 condition = A & B & C & D & E，但这实际上会转换为 ((((A & B) & C) & D) & E)，这会创建一个非常嵌套的逻辑树（见下图中的(1)），调试起来非常困难。相反，conjoin([A, B, C, D, E]) 可以创建一个扁平的树（见下图中的(2)）。

命题符号命名（重要！）

在项目的后续部分，请使用以下变量命名规则：

  • 引入变量时，必须以大写字母开头（包括 Expr）。
  • 变量名中只能出现以下字符：A-Z、a-z、0-9、_、^、[、]。
  • 逻辑连接字符 (&, |) 不得出现在变量名中。例如，Expr('A & B') 是非法的，因为它试图创建一个名为 'A & B' 的常量符号。应使用 Expr('A') & Expr('B') 来创建逻辑表达式。

Pacphysics 符号

  • PropSymbolExpr(pacman_str, x, y, time=t)：表示 Pacman 是否在时间 t 处于 (x,y)，写作 P[x,y]_t。
  • PropSymbolExpr(wall_str, x, y)：表示 (x,y) 处是否有墙，写作 WALL[x,y]。
  • PropSymbolExpr(action, time=t)：表示 Pacman 是否在时间 t 采取 action 动作，其中 action 是 DIRECTIONS 的元素，例如 North_t。
  • 一般情况下，PropSymbolExpr(str, a1, a2, a3, a4, time=a5) 创建表达式 str[a1,a2,a3,a4]_a5，其中 str 是一个字符串。

logic.py 文件中有关于 Expr 类的更多详细文档。

SAT 求解器

一个SAT（可满足性）求解器接受编码世界规则的逻辑表达式，并返回一个满足该表达式的模型（逻辑符号的真值分配），如果存在这样的模型。为了高效地从表达式中找到可能的模型，我们利用 pycosat 模块，这是 picoSAT 库的Python包装器。

运行conda install pycosat 安装。

测试pycosat安装：

在 logic 目录下运行：

python pycosat_test.py

这应该输出：

[1, -2, -3, -4, 5]

如果你在环境设置过程中遇到问题，请告知我们。这对于完成项目至关重要，我们不希望你在安装过程中浪费时间。

Q1: Logic Warm-up

这个问题将让你练习使用项目中用于表示命题逻辑句子的 Expr 数据类型。你将在 logicPlan.py 中实现以下函数：

  • sentence1(): 创建一个 Expr 实例，表示以下三个句子为真的命题。不要进行任何逻辑简化，只需按此顺序将它们放入列表中，并返回列表的合取。列表中的每个元素应该对应这三个句子中的每一个: A \vee B, \neg A \leftrightarrow (\neg B \vee C), \neg A \vee \neg B \vee C
  • sentence2(): 创建一个Expr实例，表示以下四个句子为真的命题。同样，不要进行任何逻辑简化，只需按此顺序将它们放入列表中，并返回列表的合取: C \leftrightarrow (B \vee D), A \to (\neg B \wedge \neg D), \neg(B \wedge \neg C) \to A, \neg D \to C
  • sentence3(): 使用 PropSymbolExpr 构造函数，创建符号 'PacmanAlive_0'、'PacmanAlive_1'、'PacmanBorn_0' 和 'PacmanKilled_0'（提示：回忆一下 PropSymbolExpr(str, a1, a2, a3, a4, time=a5) 创建的表达式是 str[a1,a2,a3,a4]_a5，其中 str 是一个字符串；对于这个问题，你应该创建一些与这些字符串完全匹配的字符串）。然后，创建一个 Expr 实例，以命题逻辑的形式按顺序编码以下三个英文句子，而不进行任何简化：
    1. 如果 Pacman 在时间 1 是活着的，当且仅当他在时间 0 是活着并且他在时间 0 没有被杀死，或者他在时间 0 不是活着的并且他在时间 0 出生。
    2. 在时间 0，Pacman 不能既是活着的又出生。
    3. Pacman 在时间 0 出生。
  • findModelUnderstandingCheck():
    1. 查看 findModel(sentence) 方法的工作原理：它使用 to_cnf 将输入句子转换为合取范式（SAT求解器所需的形式），并将其传递给SAT求解器以找到满足句子（sentence）中符号的赋值，即一个模型。模型是一个 表达式中符号 的字典，并对应有 True 或 False 的赋值。通过打开 Python 交互会话并运行 from logicPlan import * 和 findModel(sentence1()) 及其他两个类似查询来测试。它们是否与预期一致？
    2. 基于上述内容，填写 findModelUnderstandingCheck 使它返回在如果允许使用小写变量时， findModel(Expr('a')) 应该会返回的结果（由于不允许使用小写变量，直接调用会报错）。不应使用 findModel 或 Expr 其他超出函数中已有的内容；只需直接重建输出。
  • entails(premise, conclusion): 仅当前提(premise)能推出结论(conclusion)时才返回 True。提示：findModel 在这里很有帮助；可以尝试反证法。
  • plTrueInverse(assignments, inverse_statement): 仅当给定赋值时，(not inverse_statement) 为真时，才返回 True。

要测试和调试代码，请运行：

python autograder.py -q q1

测试某一个小点可以运行：

python autograder.py -t test_cases/q1/correctSentence1

Q2: Logic Workout

请在 logicPlan.py 文件中实现以下三个函数（记住尽可能使用 conjoin 和 disjoin）：

  1. atLeastOne(literals): 返回一个 CNF（合取范式）中的单一表达式（Expr），该表达式仅在输入列表中的至少一个表达式为真时为真。每个输入表达式都是一个文字。

  2. atMostOne(literals): 返回一个 CNF 中的单一表达式（Expr），该表达式仅在输入列表中的最多一个表达式为真时为真。提示：使用 itertools.combinations。如果你有 n 个文字，并且最多一个为真，那么生成的 CNF 表达式应该是 \binom{n}{2} 个子句的合取。

  3. exactlyOne(literals): 使用 atLeastOne 和 atMostOne 返回一个 CNF 中的单一表达式（Expr），该表达式仅在输入列表中的恰好一个表达式为真时为真。每个输入表达式都是一个文字。

每个方法都接收一个 Expr 文字的列表，并返回一个单一的 Expr 表达式，该表达式表示输入列表中表达式之间的适当逻辑关系。附加要求是，返回的 Expr 必须是 CNF（合取范式）。在方法实现中，你不能使用 to_cnf 函数（或任何辅助函数 logic.eliminate_implications、logic.move_not_inwards 和 logic.distribute_and_over_or）。

在后续问题中实现你的计划代理（planning agents）时，不要对你的 planning agents 运行 to_cnf。这是因为 to_cnf 有时会使你的逻辑表达式变得更长，因此你要尽量减少这种效果；findModel 会在需要时执行此操作。在后续问题中，重用你对 atLeastOne(.)、atMostOne(.) 和 exactlyOne(.) 的实现，而不是从头重新设计这些函数。这样可以避免意外地创建非 CNF 基础的实现，导致速度极慢。

你可以使用 logic.pl_true 函数来测试你的表达式输出。pl_true 接收一个表达式和一个模型，并仅在表达式在给定模型下为真时返回 True。

要测试和调试你的代码，请运行：

python autograder.py -q q2

Q3: Pacphysics and Satisfiability

在这个问题中，你将实现基本的 Pacphysics 逻辑表达式，并通过构建适当的逻辑表达式知识库（KB）来证明 Pacman 应该和不该存在的位置。

在 logicPlan.py 中实现以下函数：

  1. pacmanSuccessorAxiomSingle：生成一个表达式，定义 Pacman 在时间 t 位于 (x, y) 的充分且必要条件：

    • 阅读提供的可能原因 (possible_causes) 的构造。
    • 你需要填写返回语句，它将是一个 Expr。确保在适当的地方使用 disjoin 和 conjoin。查看 SLAMSuccessorAxiomSingle 可能会有帮助，尽管那里的规则比这个函数更复杂。双向条件的较简单一方应该在左边以便于自动评分器使用。

  2. pacphysicsAxioms：生成一堆物理公理。对于时间 $t$：

    • 参数：
      • 必需的：
        • t: 时间。
        • all_coords 和 non_outer_wall_coords: (x, y) 元组的列表。
      • 可能为空：你将使用这些来调用函数。
        • walls_grid: 仅传递给 successorAxioms，描述（已知的）墙。
        • sensorModel(t: int, non_outer_wall_coords) -> Expr 返回一个描述观测规则的单一 Expr；你可以查看 sensorAxioms 和 SLAMSensorAxioms 以了解示例。
        • successorAxioms(t: int, walls_grid, non_outer_wall_coords) -> Expr 描述过渡规则，例如 Pacman 的先前位置和动作如何影响当前的位置；我们在 pacmanSuccessorAxiomSingle 中见过这个。
    • 算法：
      • 对于 all_coords 中的所有 $(x, y)$，附加以下蕴涵（if-then 形式）：如果 (x, y) 处有一堵墙，那么 Pacman 在 t 时间不在 $(x, y)$。
      • 在时间 $t$，Pacman 恰好位于 non_outer_wall_coords 的一个位置。
      • 在时间 $t$，Pacman 恰好执行 DIRECTIONS 中的一个动作。
      • 传感器：附加上调用 sensorAxioms 的结果。除了 checkLocationSatisfiability 之外的所有调用者都使用这个；如何处理不希望添加任何传感器公理的情况由你决定。
      • 过渡：附加上调用 successorAxioms 的结果。所有调用者都会使用这个。
      • 将上述每个句子添加到 pacphysics_sentences。如返回语句所示，这些句子将被合取并返回。

  3. checkLocationSatisfiability：

    • 给定一个过渡 (x0_y0，action0，x1_y1)，action1 和一个问题(problem)，编写一个函数返回一个包含两个模型的元组(model1，model2)：
      • 在 model1 中，给定 x0_y0，action0，action1，Pacman 在 t=1 时位于 $(x1, y1)$。这个模型证明 Pacman 可能在那里。如果 model1 为 False，我们知道 Pacman 肯定不在那里。
      • 在 model2 中，给定 x0_y0，action0，action1，Pacman 在 t=1 时不在 $(x1, y1)$。这个模型证明 Pacman 可能不在那里。如果 model2 为 False，我们知道 Pacman 肯定在那里。
    • action1 对确定 Pacman 是否在位置上没有影响；它只是在使你的解决方案与自动评分器解决方案匹配。
    • 要实现这个问题，你需要向你的 KB 添加以下表达式：
      • 向 KB 添加：pacphysics_axioms(...)，以及适当的时间。没有 sensorModel，因为我们知道吃豆人世界上的一切。需要时，使用 allLegalSuccessorAxioms 进行过渡，因为这是针对常规 Pacman 过渡规则。
      • 向 KB 添加：Pacman 的当前位置 (x0, y0)
      • 向 KB 添加：Pacman 执行 action0
      • 向 KB 添加：Pacman 执行 action1
      • 使用 findModel 对上述两个模型进行查询。查询应该是不同的；关于如何进行查询，请参见 entails。

提醒：表示 Pacman 在时间 t 位于 (x, y) 的变量是 PropSymbolExpr(pacman_str, x, y, time=t)，表示 (x, y) 处有墙的是 PropSymbolExpr(wall_str, x, y)，表示在 t 时间执行动作 action 的是 PropSymbolExpr(action, time=t)。

要测试和调试你的代码，请运行：

python autograder.py -q q3

Q4: Path Planning with Logic

Pacman 正试图找到迷宫的终点（目标位置）。使用命题逻辑实现以下方法，为 Pacman 计划一系列行动，使其到达目标：

注意：从现在起，这些方法将会相当慢。这是因为SAT求解器非常通用，仅仅是处理逻辑，不像我们之前的算法那样使用针对特定问题的特定人类创建的算法。值得注意的是，pycosat 的实际算法是用 C 语言编写的，C 语言通常比 Python 快得多，即便如此，速度仍然很慢。

positionLogicPlan(problem)：给定一个 logicPlan.PlanningProblem 的实例，返回 Pacman 执行的一系列动作字符串。

你不会实现搜索算法，而是创建代表所有可能位置在每个时间处的 pacphysics 的表达式。这意味着在每个时间，你应该为网格上的所有可能位置添加通用规则，这些规则不假设 Pacman 的当前位置。

你需要为知识库编写以下句子，形式如下：

  • 添加到知识库：

    • 初始知识：时间 0 时Pacman的初始位置。

  • 循环（时间范围为 50，因为自动评分器不会测试需要 ≥50 时间的布局）：

    • 打印时间：查看代码运行情况以及运行到何处。
    • 初始知识：时间 t 时，Pacman 只能在 non_wall_coords 中的一个（exactlyOne）位置。这类似于 pacphysicsAxioms，但不要使用该方法，因为在生成可能位置列表时我们使用的是 non_wall_coords（稍后使用 walls_grid）。
    • 知识库中现有变量是否存在满足赋值？使用 findModel 并传入目标断言和知识库。
      • 如果存在，使用 extractActionSequence 从起点到目标返回一系列动作。
      • 目标断言是在时间 t 时 Pacman 位于目标的位置的表达式。

  • 添加到知识库：

    • Pacman 每个时间执行一个动作。
    • 过渡模型句子：为 non_wall_coords 中所有可能的 Pacman 位置调用 pacmanSuccessorAxiomSingle(...)。

请注意，根据我们设置 Pacman 网格的方式，Pacman 可占据的最左下角的空间（假设那里没有墙）是 $(1,1)$，而不是 $(0,0)$，如下所示。

Pacphysics 在 Q3 和 Q4 中的总结（也见于AIMA第7.7章）：

  • 对于所有 $x, y, t$：如果 (x, y) 处有墙，则Pacman在 t 时间不在 $(x, y)$。
  • 对于每个 $t$：Pacman恰好在所有可能的 (x, y) 位置之一。可以通过外部或所有墙的知识进行优化，按照每个函数的规范。
  • 对于每个 $t$：Pacman恰好执行一个可能的动作。
  • 对于每个 $t$（除 t = ?? 外）：过渡模型：Pacman在 t 时间在 (x, y) 当且仅当他在 t-1 时间在 (x-dx, y-dy) 并在 t-1 时间执行了 (dx, dy) 动作。

在较小的迷宫上测试代码：

python pacman.py -l maze2x2 -p LogicAgent -a fn=plp
python pacman.py -l tinyMaze -p LogicAgent -a fn=plp

要测试和调试你的代码，请运行：

python autograder.py -q q4

调试提示：

  • 如果你发现解决方案长度为 0 或 1：仅仅知道Pacman在给定时间的位置是否足够？是什么阻止他同时出现在其他地方？
  • 作为理智检查，验证如果Pacman在时间 0 在 $(1,1)$，并在时间 6 在 $(4,4)$，他在此期间从未在 $(5,5)$。
  • 如果解决方案运行时间超过几分钟，你可能需要重新审视 exactlyOne 和 atMostOne 的实现，并确保使用尽可能少的子句。

Q5: Eating All the Food

Pacman 试图吃掉棋盘上的所有食物。使用命题逻辑实现以下方法，为 Pacman 计划一系列行动，使其达到目标。

foodLogicPlan(problem)：给定一个 logicPlan.PlanningProblem 实例，返回 Pacman 执行的一系列动作字符串。

这个问题的总体格式与问题 4 相同；你可以从那里复制你的代码作为起点。问题 4 的注释和提示也适用于这个问题。你需要实现以前问题中未实现的所有必要的后继状态公理。

与前一问题的变化：

  • 初始化 Food[x,y]_t 变量，根据初始信息使用代码 PropSymbolExpr(food_str, x, y, time=t)，当且仅当 t 时间 (x, y) 处有食物时，每个变量为真。
  • 改变目标断言：你的目标断言句子必须在且仅在所有食物都被吃掉时为真。当所有 Food[x,y]_t 为假时发生。
  • 添加食物后继公理：Food[x,y]_t+1 和 Food[x,y]_t 以及 Pacman[x,y]_t 之间的关系是什么？食物后继公理只应涉及这三个变量，对于任何给定的 (x, y) 和 $t$。考虑食物变量的过渡模型，并在每个时间步将这些句子添加到你的知识库中。

测试代码：

python pacman.py -l testSearch -p LogicAgent -a fn=flp,prob=FoodPlanningProblem

我们不会在需要超过 50 个时间的布局上测试你的代码。

测试和调试代码：

python autograder.py -q q5

其余项目的辅助函数

对于剩下的问题，我们将依赖以下辅助函数，这些函数将在定位、建图和SLAM的伪代码中引用。

将 pacphysics、动作和感知信息添加到 KB：
  • 添加到 KB：pacphysics_axioms(...)（你在Q3中编写的）。使用 sensorAxioms 和 allLegalSuccessorAxioms 进行定位和建图，只在 SLAM 中使用 SLAMSensorAxioms 和 SLAMSuccessorAxioms。
  • 添加到 KB：Pacman 采取由 agent.actions[t] 规定的动作。
  • 通过调用 agent.getPercepts() 获取感知并将感知传递给 fourBitPerceptRules(...) 以进行定位和建图，或传递给 numAdjWallsPerceptRules(...) 以进行SLAM。将生成的 percept_rules 添加到 KB。
使用更新的 KB 查找可能的 Pacman 位置：
  • possible_locations = []
  • 遍历 non_outer_wall_coords。
    • 我们能否证明 Pacman 在 (x, y) 处？我们能否证明 Pacman 不在 (x, y) 处？使用 entails 和 KB。
    • 如果存在满足赋值的情况，在时间 t Pacman 在 $(x, y)$，则将 (x, y) 添加到 possible_locations。
    • 添加到 KB：在时间 t Pacman 明确在的位置 $(x, y)$。
    • 添加到 KB：在时间 t Pacman 明确不在的位置 $(x, y)$。
    • 提示：检查 entails 的结果是否相互矛盾（即 KB entails A 和 entails ¬A）。如果是，打印反馈以帮助调试。
使用更新的 KB 查找可证明的墙位置：

  • 遍历 non_outer_wall_coords。

    • 我们能否证明 (x, y) 处有墙？我们能否证明 (x, y) 处没有墙？使用 entails 和 KB。
    • 添加到 KB 并更新 known_map：明确有墙的位置 $(x, y)$。
    • 添加到 KB 并更新 known_map：明确没有墙的位置 $(x, y)$。
    • 提示：检查 entails 的结果是否相互矛盾（即 KB entails A 和 entails ¬A）。如果是，打印反馈以帮助调试。

    观察：我们将已知的 Pacman 位置和墙添加到 KB，以便在后续时间步中不必重新查找这些内容；从技术上讲，这是冗余信息，因为我们首先使用 KB 证明了这一点。

Q6: Localization

Pacman 从已知地图开始，但起始位置未知。它有一个 4-bit 的传感器，返回其在北、南、东、西方向上是否有墙。例如，1001 表示 Pacman 的北和西方向有墙，这 4 位用有 4 个布尔值的列表表示。通过记录这些传感器读数以及每个时间采取的动作，Pacman能够确定其位置。你需要编写帮助 Pacman 确定每个时间可能位置的句子，通过实现：

localization(problem, agent)：给 定 logicPlan.LocalizationProblem 的一个实例和 logicAgents.LocalizationLogicAgent 的一个实例，在时间 0 到 agent.num_steps-1 之间重复生成在时间 t 可能的位置列表 $(x_i, y_i)$：[ (x_0_0, y_0_0), (x_1_0, y_1_0), ...]。注意，你不需要担心生成器的工作方式，因为这行代码已经为你写好了。

为了让 Pacman 在定位过程中使用传感器信息，你将使用已经为你实现的两个方法。sensorAxioms, 即 Blocked[Direction]_t \leftrightarrow [(P[x_i,y_j]_t\wedge WALL[x_i+dx,y_j+dy])\vee (P[x_i',y_j']_t\wedge WALL[x_i'+dx,y_j'+dy])...] 和 fourBitPerceptRules，它们将时间t的感知转换为逻辑句子。

请按照我们的伪代码实现该函数：

  • 添加到知识库：墙所在的位置（walls_list）和不在的位置（not in walls_list）。
  • 对于在 range(agent.num_timesteps) 中的 $t$：
    • 添加 pacphysics、动作和感知信息到知识库。
    • 使用更新的知识库查找可能的 Pacman 位置。
    • 在时间 t 上调用 agent.moveToNextState(action_t)。
    • 生成（yield）可能的位置。

关于显示：黄色的 Pacman 是在当前的时间的位置，白色的是由已知的墙和自由空间等计算的上一个时间的可能的位置。

测试和调试代码：

python autograder.py -q q6

Q7: Mapping

Pacman 现在知道了他的起始位置，但不知道墙的位置（除了外部坐标的边界是墙）。与定位类似，它有一个4位的传感器，返回其在北、南、东、西方向上是否有墙。你将编写帮助Pacman确定墙位置的句子，通过实现：

mapping(problem, agent)：给定一个 logicPlan.MappingProblem 的实例和一个 logicAgents.MappingLogicAgent 的实例，在时间 0 到 agent.num_steps-1 之间重复生成关于地图的信息 [[1, 1, 1, 1], [1, -1, 0, 0], ...]。注意，你不需要担心生成器的工作方式，这行代码已经为你写好了。

known_map：

  • known_map 是一个大小为 (problem.getWidth()+2, problem.getHeight()+2) 的二维数组（列表的列表），因为地图周围有墙。
  • 如果 (x, y) 在时间 t 保证是墙，则 known_map 的每个条目为 1；如果保证不是墙则为 0；如果 (x, y) 在时间 t 仍然不明确，则为 -1。
  • 当无法证明 (x, y) 是墙，也无法证明 (x, y) 不是墙时，结果是不明确的。

请按照我们的伪代码实现该函数：

  1. 获取 Pacman 的初始位置 (pac_x_0, pac_y_0)，并将其添加到知识库中。同时添加该位置是否有墙。
  2. 对于 t 在 range(agent.num_timesteps) 中：
    • 添加 pacphysics、动作和感知信息到知识库。
    • 使用更新的知识库查找可证明的墙位置。
    • 在时间 t 上调用 agent.moveToNextState(action_t)。
    • 生成 known_map。

测试和调试代码：

python autograder.py -q q7

有时，Pacman 在迷失和黑暗中徘徊。 在 SLAM（同时定位与建图）中，Pacman 知道他的初始坐标，但不知道墙的位置。在 SLAM 中，Pacman 可能会无意中采取非法动作（例如，当北面有墙阻挡时向北走），这会增加 Pacman 随时间的不确定性。此外，在我们的 SLAM 设置中，Pacman 不再有一个4位的传感器来告诉我们四个方向是否有墙，而是只有一个 3-bit 的传感器，揭示他附近有多少墙。这有点像 WiFi 信号强度条；000 表示没有邻近的墙，100 表示恰好有1面墙相邻，110 表示恰好有2面墙相邻，111 表示恰好有3面墙相邻。这 3 位由 3 个布尔值的列表表示。因此，你将使用 SLAMSensorAxioms 和 numAdjWallsPerceptRules，而不是 sensorAxioms 和 fourBitPerceptRules。你将编写帮助 Pacman 确定以下内容的句子：（1）每个时间的可能位置，（2）墙的位置，具体实现方法如下：

slam(problem, agent)：给定一个 logicPlan.SLAMProblem 和 logicAgents.SLAMLogicAgent 的实例，重复生成一个包含两个项目的元组：

  • 时间 t 的 known_map（格式与问题6中的 mapping 相同）
  • 时间 t 的 Pacman 可能位置的列表（格式与问题5中的 localization 相同）

为了通过自动评分器，请按照我们的伪代码实现该函数：

  1. 获取 Pacman 的初始位置 (pac_x_0, pac_y_0)，并将其添加到知识库（KB）中。相应更新 known_map 并将适当的表达式添加到知识库。
  2. 对于 t 在 range(agent.num_timesteps) 中：
    • 添加 pacphysics、动作和感知信息到知识库。使用 SLAMSensorAxioms、SLAMSuccessorAxioms 和 numAdjWallsPerceptRules。
    • 使用更新的知识库查找可证明的墙位置。
    • 使用更新的知识库查找可能的 Pacman 位置。
    • 在时间 t 上调用 agent.moveToNextState(action_t)。
    • 生成 known_map 和 possible_locations。

测试和调试代码（注意：这可能很慢）：

python autograder.py -q q8